問題を解くのに必要な知識を確認するにはこのグラフ図を利用してください．

2次関数のグラフの拡大に関する問題

■問題

2次関数${\displaystyle y=x^2}$ のグラフを原点を中心にy 軸方向に ${\displaystyle -\frac{1}{2}}$  倍した（拡大した）グラフを表す関数を求めよ．

■答

${\displaystyle y=-\frac{1}{2}{x}^2}$

■解説

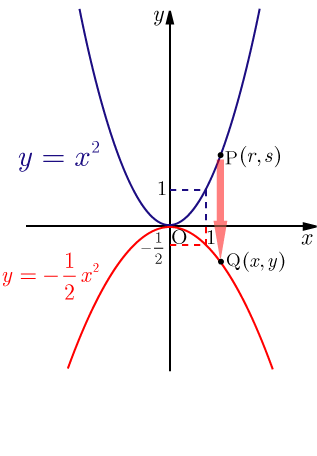関数${\displaystyle y=f\left(x\right)}$ のグラフを原点を中心としてx 軸方向にc 倍 ，y 軸方向にd 倍したグラフを表す関数は

${\displaystyle \frac{y}{d}=f\left(\frac{x}{c}\right)}$ 　

となる(グラフの拡大を参照)．今回は${\displaystyle c=1}$  ，${\displaystyle d=-\frac{1}{2}}$ に対応する．よって${\displaystyle y=x^2}$ を

${\displaystyle x\to \frac{x}{1}}$，${\displaystyle y\to \frac{y}{-\frac{1}{2}}}$

に書き換えて

${\displaystyle \frac{y}{-\frac{1}{2}}=x^2}$

${\displaystyle y=-\frac{1}{2}{x}^2}$

となる．これが求める関数である．

 

ホーム>>カテゴリー分類>>関数>>関数の演習問題>>グラフの移動に関する問題>>2次関数のグラフの拡大に関する問題

最終更新日： 2024年9月13日

[ページトップ]

利用規約

google translate (English version)