三角関数のグラフに関する問題
■問題
次の三角関数のグラフを描け.
■解答
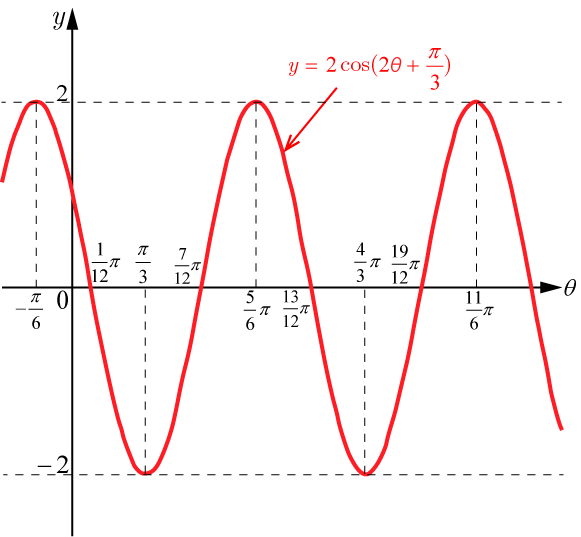
■ヒント
を描くには,次の手順で拡大や縮小,平行移動する.
のグラフの場合,
-
とする
- を原点を中心として
軸方向に
倍に拡大・縮小して
を描く.
- を原点を中心として軸方向に倍
に拡大・縮小してを描く.
-
を軸方向に
平行移動して
を描く.
■解説
-
とする.
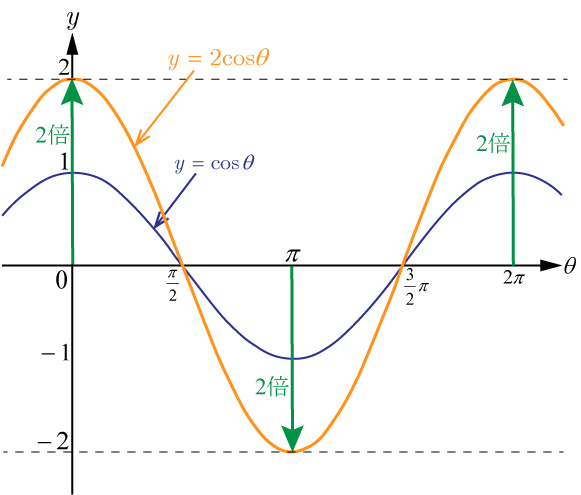
- を原点を中心として
軸方向に
倍に拡大して
を描く.
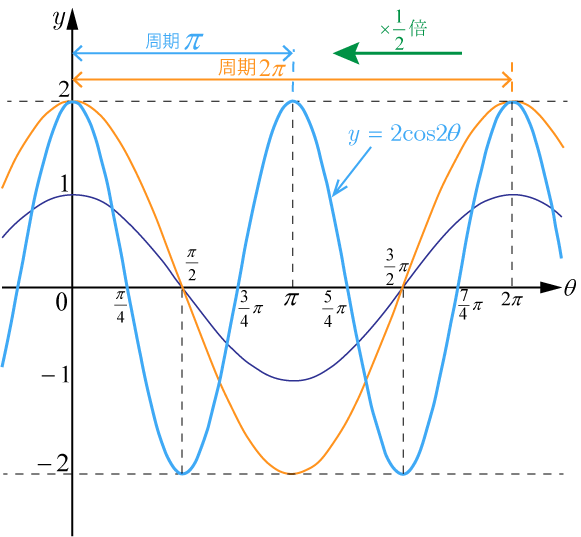
- を原点を中心として軸方向に倍
に縮小してを描く.
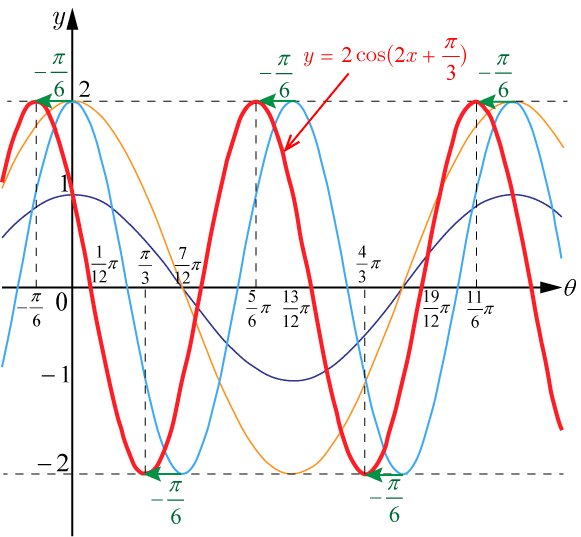
-
を軸方向に
平行移動して
を描く.
ホーム>>カテゴリー分類>>三角関数>>三角関数の問題>>三角関数のグラフ>>問題
学生スタッフ作成
最終更新日:
2025年3月17日