■解法のヒント

■new YouTube動画

■三角関数

■ベクトル

■指数/対数

■微分方程式

■級数展開

■線形代数

■ラプラス変換

■チャットボット

問題を解くのに必要な知識を確認するにはこのグラフ図を利用してください．

三角関数のグラフに関する問題

■問題

$y = \sin (θ - \frac{π}{4})$ ， $y = \sin (θ + \frac{π}{4})$ のグラフを描け

■解説動画

◆三角関数の動画一覧のページへ

■答

■ヒント

単位円を描き，グラフの平行移動に注意してグラフを描く．

■解説

● $y = \sin (θ - \frac{π}{4})$ のグラフ

グラフの平行移動の式より， $y = \sin θ$ のグラフを $θ$ 軸方向に $a$ 平行移動したグラフを表す式は， $y = \sin (θ - a)$ となる．このことより

$y = \sin (θ - \frac{π}{4})$ のグラフは

$θ$ 軸方向に $y = \sin θ$ のグラフを $\frac{π}{4}$ 平行移動したもの

になる．

$θ$	$0$	$\frac{1}{4} π$	$\frac{1}{2} π$	$\frac{3}{4} π$	$π$	$\frac{5}{4} π$	$\frac{3}{2} π$	$\frac{7}{4} π$	$2 π$
$θ + \frac{1}{4} π$	$\frac{1}{4} π$	$\frac{1}{2} π$	$\frac{3}{4} π$	$π$	$\frac{5}{4} π$	$\frac{3}{2} π$	$\frac{7}{4} π$	$2 π$	$\frac{9}{4} π$
$\sin θ$	$0$	$\frac{\sqrt{2}}{2}$	$1$	$\frac{\sqrt{2}}{2}$	$0$	$- \frac{\sqrt{2}}{2}$	$- 1$	$- \frac{\sqrt{2}}{2}$	$0$
$\sin (θ + \frac{1}{4} π)$	$\frac{\sqrt{2}}{2}$	$1$	$\frac{\sqrt{2}}{2}$	$0$	$- \frac{\sqrt{2}}{2}$	$- 1$	$- \frac{\sqrt{2}}{2}$	$0$	$\frac{\sqrt{2}}{2}$

● $y = \sin (θ + \frac{π}{4})$ のグラフ

$y = \sin (θ + \frac{π}{4})$ を書き換えると $y = \sin (θ - (- \frac{π}{4}))$ となる．よって

$y = \sin (θ + \frac{π}{4})$ のグラフは

$y = \sin θ$ のグラフをを $θ$ 軸方向に $- \frac{π}{4}$ 平行移動したもの

になる．

$θ$	$0$	$\frac{1}{4} π$	$\frac{1}{2} π$	$\frac{3}{4} π$	$π$	$\frac{5}{4} π$	$\frac{3}{2} π$	$\frac{7}{4} π$	$2 π$
$θ - \frac{1}{4} π$	$- \frac{1}{4} π$	$0$	$\frac{1}{4} π$	$\frac{1}{2} π$	$\frac{3}{4} π$	$π$	$\frac{5}{4} π$	$\frac{3}{2} π$	$\frac{7}{4} π$
$\sin θ$	$0$	$\frac{\sqrt{2}}{2}$	$1$	$\frac{\sqrt{2}}{2}$	$0$	$- \frac{\sqrt{2}}{2}$	$- 1$	$- \frac{\sqrt{2}}{2}$	$0$
$\sin (θ - \frac{1}{4} π)$	$- \frac{\sqrt{2}}{2}$	$0$	$\frac{\sqrt{2}}{2}$	$1$	$\frac{\sqrt{2}}{2}$	$0$	$- \frac{\sqrt{2}}{2}$	$- 1$	$- \frac{\sqrt{2}}{2}$

●２つのグラフをまとめたもの

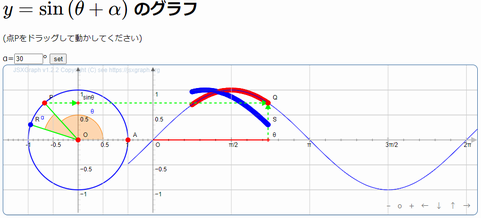
■インターラクティブなグラフ

画像をクリックしてください．

ホーム>>カテゴリー分類>>三角関数>>問題演習

学生スタッフ作成

最終更新日： 2025年4月27日

[ページトップ]

$金沢工業大学$

google translate (English version)