|
|||||||||||||
|
|||||||||||||
|
問題を解くのに必要な知識を確認するにはこの知識グラフを利用してください.
円錐の重心の計算
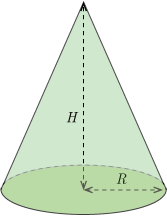
■問題
図のような底面の半径が ,高さが の円錐の重心を求めよ.
■答
円錐の底面より高さ の位置
■ヒント
回転体の重心を参考にする.
■解説
図のように円錐の対称軸が 軸と重なるようにし,円錐の頂点を原点とする.
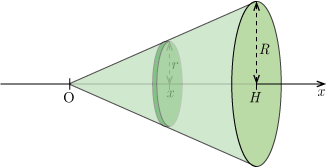
軸の位置 における軸に垂直で厚さが微小な,半径が の円板の体積は
・・・・・・(1)
となる.また, より
・・・・・・(2)
となる.よって,(2)を(1)に代入すると
となる.重心は 軸上にあるので,重心の 座標を とすると
となる.
よって,重心の位置は,円錐の底面より高さ の位置にある.
ホーム>>カテゴリー分類>>積分>>積分の問題>>定積分の問題>>円錐の重心の計算
最終更新日: 2023年11月23日