|
|||||||||||||
|
|||||||||||||
|
関連するページを見るにはこのグラフ図を利用してください．
特異解 (singular solution)
微分方程式よっては，その微分方程式の一般解の任意定数にどのような値を代入しても得られない付加的な解をもつことがあり，それを 特異解 (singular solution) という．
※ 一般解の任意定数に適当な値を代入した特殊解とは違うものであることに注意！
■例
(y′)2+4xy′−4y=0
一般解：
y=2cx+c2
（c：任意定数）
特異解：
y=−x2
（この微分方程式の一般解，特異解の求め方）
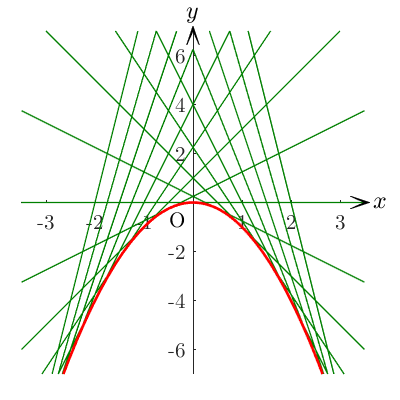
一般解 y=2cx+c2 は傾き 2c ，切片 c2 の直線の方程式を表し，任意定数 c に適当な値を代入した特殊解のグラフを図の緑線で示す．
特異解 y=−x2 は上に凸の放物線であり，そのグラフを図の赤線で示す．一般解 y=2cx+c2 の任意定数 c にどのような値を代入しても特異解は得られない．
このように，微分方程式によっては特異解をもつことがあり，その場合，一般解を求めたからといってすべての解を求めたことにはならない．
