曲率

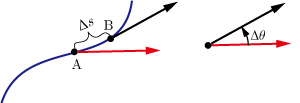
曲線の曲がり具合を示す量が曲率 $κ$ である．曲線上の点Ａからに沿って $Δ s$ 移動し点Ｂに達したとする．点Ａでの移動方向と点Ｂでの移動方向の角度の変化量を $Δ θ$ とする．角度の変化は進行方向に対して左回り（反時計回り）に変化する場合を正とする．曲率 $κ$ は

$κ = \lim_{Δ s \to 0} \frac{Δ θ}{Δ s}$

と定義される．すなわち，曲率 $κ$ は曲線上の点の移動距離に関する進行移動方向の変化率である．

曲線が $y = f (x)$ で表される場合，曲線上の点 $(x_{A}, f (x_{A}))$ における曲率 $κ$ は

$κ = \frac{f^{″} (x_{A})}{{[1 + {f^{'} (x_{A})}^{2}]}^{\frac{3}{2}}}$

となる．

導出

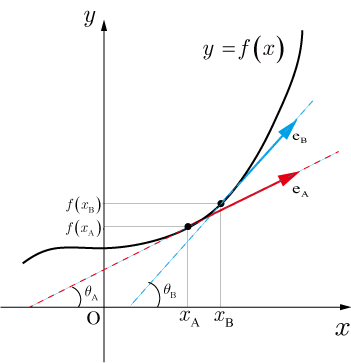
点Aでの移動方向を単位ベクトルで表したものを ${\vec{e}}_{A}$ ，点Bでの移動距離を単位ベクトルで表したものを ${\vec{e}}_{B}$ とし， $x$ 軸と ${\vec{e}}_{A}$ のなす角を $θ_{A}$ ， $x$ 軸と ${\vec{e}}_{B}$ のなす角を $θ_{B}$ とする．

$Δ θ = θ_{B} - θ_{A}$

$\tan Δ θ = \tan (θ_{B} - θ_{A})$

正接関数の加法定理より

$= \frac{\tan θ_{B} - \tan θ_{A}}{1 + \tan θ_{B} \tan θ_{A}}$

$\tan θ_{A} = f^{'} (x_{A}), \tan θ_{B} = f^{'} (x_{B})$ より

$= \frac{f^{'} (x_{B}) - f^{'} (x_{A})}{1 + f^{'} (x_{B}) f^{'} (x_{A})}$

逆正接関数を用いると,

$Δ θ = \tan^{- 1} \frac{f^{'} (x_{B}) - f^{'} (x_{A})}{1 + f^{'} (x_{B}) f^{'} (x_{A})}$

$\tan^{- 1} x$ のマクローリン展開 $\tan^{- 1} x = x - \frac{1}{3} x^{3} + \frac{1}{5} x^{5} - \dots$ より

$= \frac{f^{'} (x_{B}) - f^{'} (x_{A})}{1 + f^{'} (x_{B}) f^{'} (x_{A})} - \frac{1}{3} {(\frac{f^{'} (x_{B}) - f^{'} (x_{A})}{1 + f^{'} (x_{B}) f^{'} (x_{A})})}^{3} + \frac{1}{5} {(\frac{f^{'} (x_{B}) - f^{'} (x_{A})}{1 + f^{'} (x_{B}) f^{'} (x_{A})})}^{5} - \dots$

一方,積分の平均値の定理より

$f (x_{C}) = \frac{1}{x_{B} - x_{A}} \int_{x_{A}}^{x_{B}} f (x) d x$

$\sqrt{1 + {f^{'} (x_{C})}^{2}} = \frac{1}{x_{B} - x_{A}} \int_{x_{A}}^{x_{B}} \sqrt{1 + {f^{'} (x)}^{2}} d x$

が成り立つ

よって

$Δ s = \int_{x_{A}}^{x_{B}} \sqrt{1 + {f^{'} (x)}^{2}} dx$ $= \sqrt{1 + {f^{'} (x_{C})}^{2}} (x_{B} - x_{A})$

$Δ s \to 0$ のとき $x_{B} \to x_{A}$ となる。

よって曲率Kは,

$K = \lim_{Δ s \to 0} \frac{Δ θ}{Δ s}$

$= \lim_{x_{B} \to x_{A}} \frac{1}{\sqrt{1 + {f^{'} (x_{C})}^{2}} (x_{B} - x_{A})} {\frac{f^{'} (x_{B}) - f^{'} (x_{A})}{1 + f^{'} (x_{A}) f^{'} (x_{B})} - \frac{1}{3} {(\frac{f^{'} (x_{B}) - f^{'} (x_{A})}{1 + f^{'} (x_{A}) f^{'} (x_{B})})}^{3} + \frac{1}{5} {(\frac{f^{'} (x_{B}) - f^{'} (x_{A})}{1 + f^{'} (x_{A}) f^{'} (x_{B})})}^{5} - \dots}$

$= \lim_{x_{B} \to x_{A}} \frac{1}{\sqrt{1 + {f^{'} (x_{C})}^{2}} (x_{B} - x_{A})} \cdot \frac{f^{'} (x_{B}) - f^{'} (x_{A})}{1 + f^{'} (x_{A}) f^{'} (x_{B})} {1 - \frac{1}{3} {(\frac{f^{'} (x_{B}) - f^{'} (x_{A})}{1 + f^{'} (x_{A}) f^{'} (x_{B})})}^{2} + \frac{1}{5} {(\frac{f^{'} (x_{B}) - f^{'} (x_{A})}{1 + f^{'} (x_{A}) f^{'} (x_{B})})}^{4} - \dots}$

$x_{B} \to x_{A}$ のとき $x_{C} \to x_{A}$ また,導関数の定義より

$\lim_{x_{B} \to x_{A}} \frac{f^{'} (x_{B}) - f^{'} (x_{A})}{1 + f^{'} (x_{A}) f^{'} (x_{B})} = 0$

$\lim_{x_{B} \to x_{A}} \frac{f^{'} (x_{B}) - f^{'} (x_{A})}{x_{B} - x_{A}} = f^{″} (x_{A})$

が成り立つ

よって

$k = \frac{1}{\sqrt{1 + {f^{'} (x_{A})}^{2}}} \cdot \frac{1}{1 + f^{'} (x_{A}) \cdot f^{'} (x_{A})} \cdot f^{″} (x_{A})$

$= \frac{f^{″} (x_{A})}{{[\sqrt{1 + {f^{'} (x_{A})}^{2}}]}^{\frac{3}{2}}}$

ホーム>>カテゴリー分類>>微分>>曲率

最終更新日：2023年5月25日