複素数の積

2つの複素数 $z_1$ ， $z_2$ の積を考える．

$z_1=x_1+y_{1}i$ ， $z_2=x_2+y_{2}i$

とおくと

${\displaystyle z_1·z_2}$ ${\displaystyle =\left(x_1+y_{1}i\right)\left(x_2+y_{2}i\right)}$

${\displaystyle =x_1{x}_2+x_1{y}_{2}i+x_2{y}_{1}i+y_1{y}_2{i}^2}$

${\displaystyle =\left(x_1{x}_2-y_1{y}_2\right)+\left(x_1{y}_2+x_2{y}_1\right)i}$

となる．しかし，計算はできたがこの積の値がどのような意味をもつのか直感的に理解できない．そこで，複素数を極形式で表し，複素数の積の意味を考えてみる．

$z_1=r_1\left(cos{\theta }_1+isin{\theta }_1\right)$ ， $z_1=r_2\left(cos{\theta }_2+isin{\theta }_2\right)$

とおくと

${\displaystyle z_1·z_2}$ ${\displaystyle =r_1{r}_2\left(cos{\theta }_1+sin{\theta }_{1}i\right)\left(cos{\theta }_2+sin{\theta }_{2}i\right)}$

${\displaystyle =r_1{r}_{2}cos{\theta }_{1}cos{\theta }_2}$ ${\displaystyle +icos{\theta }_{1}sin{\theta }_2}$ ${\displaystyle +isin{\theta }_{1}cos{\theta }_2}$ ${\displaystyle +i^{2}sin{\theta }_{1}sin{\theta }_2}$

${\displaystyle =r_1{r}_2\left(cos{\theta }_{1}cos{\theta }_2-sin{\theta }_{1}sin{\theta }_2\right)}$ ${\displaystyle +i\left(cos{\theta }_{1}sin{\theta }_2+cos{\theta }_{2}sin{\theta }_1\right)}$

三角関数の加法定理を用いると

${\displaystyle =r_1{r}_2\left\{cos\left({\theta }_1+{\theta }_2\right)+isin\left({\theta }_1+{\theta }_2\right)\right\}}$

この結果をよく見ると， $z_1·z_2$ は絶対値が $r_1·r_2$ ， 偏角が ${\theta }_1+{\theta }_2$ となっている．すなわち

複素数の積は 絶対値は積に， 偏角は和

${\displaystyle \left|z_1\cdot z_2\right|=\left|z_1\right|\cdot \left|z_2\right|}$ ， ${\displaystyle arg\left(z_1+z_2\right)=arg{z}_1+arg{z}_2}$

になる． これを図で示すと下図のようになる．

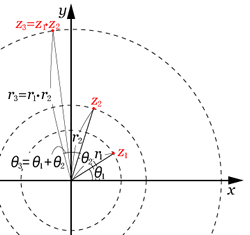
この特徴を図形問題に応用する場合が多い．

１．図形の回転

複素平面上に描いた図形の各点を示す複素数に，絶対値が1で偏角が $\theta$ の複素数 $z=cos\theta +isin\theta$ を掛けると，図形を原点 $\text{O}$ を中心に $\theta$ 回転させることができる．

２．図形の拡大／縮小

複素平面上に描いた図形の各点を示す複素数に，絶対値が $r$ ，偏角が $0$ の複素数 $z=r$ を掛けると，図形を $r$ 倍にすることができる．

３．図形の回転+拡大／縮小

複素平面上に描いた図形の各点を示す複素数に，絶対値が $r$ ，偏角が $\theta$ の複素数 $z=r\left(cos\theta +isin\theta \right)$ を掛けると，図形を 原点 $\text{O}$ を中心に $\theta$ 回転させ，かつ $r$ 倍にすることができる．

---

点 ${\displaystyle z_1}$ ，点 ${\displaystyle z_2}$ をドラッグ(タップ)して動かしてみましょう．

　

ホーム>>カテゴリー分類>>複素数 >>複素数の積

最終更新日： 2025年12月5日