3次の行列式の幾何学的解釈

3次の行列式の場合

$| A | = | \begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{matrix} |$ の1,2,3列目を，それぞれ列ベクトルとして

$a_{1} = (\begin{matrix} a_{11} \\ a_{21} \\ a_{31} \end{matrix})$ , $a_{2} = (\begin{matrix} a_{12} \\ a_{22} \\ a_{32} \end{matrix})$ ， $a_{3} = (\begin{matrix} a_{13} \\ a_{23} \\ a_{33} \end{matrix})$

とおくと， $| A |$ の絶対値は $a_{1}$ , $a_{2}$ , $a_{3}$ を3辺とする平行六面体の体積に等しい．

■導出

$| A |$ を第1列で余因子展開すると

$| A | = a_{11} | \begin{matrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{matrix} | - a_{21} | \begin{matrix} a_{12} & a_{13} \\ a_{32} & a_{33} \end{matrix} |$ $+ a_{31} | \begin{matrix} a_{12} & a_{13} \\ a_{22} & a_{23} \end{matrix} |$ $= a_{1} \cdot (\begin{matrix} |\begin{matrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{matrix}| \\ - |\begin{matrix} a_{12} & a_{13} \\ a_{32} & a_{33} \end{matrix}| \\ |\begin{matrix} a_{12} & a_{13} \\ a_{22} & a_{23} \end{matrix}| \end{matrix})$

となる．ここで

$(\begin{matrix} |\begin{matrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{matrix}| \\ - |\begin{matrix} a_{12} & a_{13} \\ a_{32} & a_{33} \end{matrix}| \\ |\begin{matrix} a_{12} & a_{13} \\ a_{22} & a_{23} \end{matrix}| \end{matrix})$ $= (\begin{matrix} a_{22} a_{33} - a_{23} a_{32} \\ - (a_{12} a_{33} - a_{13} a_{32}) \\ a_{12} a_{23} - a_{13} a_{22} \end{matrix})$ $= a_{2} \times a_{3}$ （ベクトルの外積）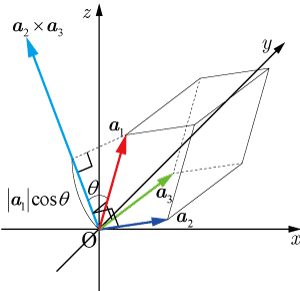

であるので，

$| A | = a_{1} \cdot (a_{2} \times a_{3})$

となる．

$a_{1}$ と $a_{2} \times a_{3}$ のなす角を $θ$ とすると

$a_{1} \cdot (a_{2} \times a_{3}) = | a_{1} | | a_{2} \times a_{3} | \cos θ$

$= | a_{2} \times a_{3} | (| a_{1} | \cos θ)$

となる． $| a_{2} \times a_{3} |$ は $a_{2}$ と $a_{3}$ を2辺とする平行四辺形の面積の値であり， $| a_{1} | \cos θ$ の絶対値は， $a_{2}$ と $a_{3}$ を2辺とする平行四辺形を底面とする平行六面体の高さである（図を見よ）．

したがって $0^{\circ} \leq θ \leq 90^{\circ}$ のとき， $| A |$ の値は $a_{1}$ , $a_{2}$ , $a_{3}$ を3辺とする平行六面体の体積の値となり， $90^{\circ} < θ \leq 180^{\circ}$ のとき， $| A |$ の値は上記体積の値に $- 1$ をかけたものになる．

ホーム>>カテゴリー分類>>行列>>線形代数>>行列式の幾何学的解釈

学生スタッフ作成

最終更新日： 2022年6月26日