2次の行列式の幾何学的な意味

2次の行列式の場合

行列式${\displaystyle \left|A\right|=\left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|}$ の1列目と2列目を，それぞれ列ベクトルとして

${\displaystyle a_1=\left(\begin{array}{c}{a}_{11}\\ a_{21}\end{array}\right)}$ ，${\displaystyle a_2=\left(\begin{array}{c}{a}_{12}\\ a_{22}\end{array}\right)}$

とおくと，${\displaystyle \left|A\right|}$ の絶対値は平面ベクトル ${\displaystyle a_1}$ , ${\displaystyle a_2}$ を2辺とする平行四辺形の面積の値に等しい．

■導出

${\displaystyle \left(\begin{array}{c}{a}_{11}\\ a_{21}\end{array}\right)=a_1}$ ，${\displaystyle \left(\begin{array}{c}{a}_{12}\\ a_{22}\end{array}\right)=a_2}$

とおく．

${\displaystyle \left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|}$${\displaystyle =a_{11}{a}_{22}-a_{12}{a}_{21}=a_{11}{a}_{22}+a_{21}\left(-a_{12}\right)}$

と変形し，

${\displaystyle \left(\begin{array}{c}{a}_{22}\\ -a_{12}\end{array}\right)={{\mathit{a}}_2}^{\prime }}$

とおくと，

${\displaystyle \left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|=a_1·{a_2}^{\prime }}$

となる．行列式は${\displaystyle a_1}$と${\displaystyle {a_2}^{\prime }}$の内積で表わされる．

${\displaystyle a_2}$と${\displaystyle {a_2}^{\prime }}$の関係を行列を使って表わす．

${\displaystyle a_{22}=0·a_{12}+1·a_{22}}$

${\displaystyle -a_{12}=-1·a_{12}+0·a_{22}}$

より

${\displaystyle \left(\begin{array}{c}{a}_{22}\\ -a_{12}\end{array}\right)=\left(\begin{array}{c}0·a_{12}+1·a_{22}\\ -1·a_{12}+0·a_{22}\end{array}\right)}$

${\displaystyle =\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)\left(\begin{array}{c}{a}_{12}\\ a_{22}\end{array}\right)}$

となる．

行列${\displaystyle \left(\begin{array}{cc}\cos \left(-{90}^{\circ }\right)& -\sin \left(-{90}^{\circ }\right)\\ \sin \left(-{90}^{\circ }\right)& \cos \left(-{90}^{\circ }\right)\end{array}\right)}$は原点を中心に${\displaystyle -{90}^{\circ }}$反時計回り，（${\displaystyle {90}^{\circ }}$時計回り）に回転させる回転行列である．

すなわち${\displaystyle {a_2}^{\prime }}$は${\displaystyle a_2}$の始点を回転の中心として時計回りに${\displaystyle {90}^{\circ }}$回転させたベクトルになる．

${\displaystyle a_1}$，${\displaystyle a_2}$，${\displaystyle {a_2}^{\prime }}$を座標平面に描くと図のようになる．

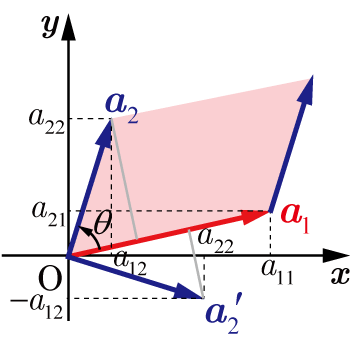
${\displaystyle a_1}$を原点を中心を反時計回りに回転させ${\displaystyle a_2}$重ねた時の回転角を${\displaystyle \theta }$ とすると，${\displaystyle a_1}$と${\displaystyle a_2}$のなす角は${\displaystyle \left|\theta \right|}$（ただし，${\displaystyle -180°\le \theta \le 180°}$） となる．${\displaystyle a_1}$と${\displaystyle {a_2}^{\prime }}$のなす角は，${\displaystyle -90°\le \theta \le 180°}$ の時，${\displaystyle \left|\theta -90°\right|}$，${\displaystyle -180°\le \theta <-90°}$の時，${\displaystyle \left|\theta +270°\right|}$ となる．

●${\displaystyle -90°\le \theta \le 180°}$で${\displaystyle a_1}$と${\displaystyle {a_2}^{\prime }}$のなす角が${\displaystyle \left|\theta -90°\right|}$の場合

${\displaystyle \left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|=a_1·{a_2}^{\prime }}$

${\displaystyle =\left|a_1\right|\left|{a_2}^{\prime }\right|\cos \left(\left|\theta -90°\right|\right)}$

${\displaystyle =\left|a_1\right|\left|{a_2}^{\prime }\right|\cos \left(\theta -90°\right)}$

${\displaystyle =\left|a_1\right|\left|{a_2}^{\prime }\right|\sin \theta }$

（${\displaystyle \because \left|{a_2}^{\prime }\right|=\left|a_2\right|}$，${\displaystyle \cos \left({90}^{\circ }-\theta \right)=\cos \left(\theta -{90}^{\circ }\right)=\sin \theta }$ 　⇒ここを参照）

${\displaystyle =\left|$ {\displaystyle a_1}$\right|\left(\left|a_2\right|\sin \theta \right)}$　･･････(1)

●${\displaystyle -180°\le \theta <-90°}$で${\displaystyle a_1}$と${\displaystyle {a_2}^{\prime }}$のなす角が${\displaystyle \left|\theta +270°\right|}$ の場合

${\displaystyle \left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|=a_1·{a_2}^{\prime }}$

${\displaystyle =\left|a_1\right|\left|{a_2}^{\prime }\right|\cos \left(\left|\theta +270°\right|\right)}$

${\displaystyle =\left|a_1\right|\left|{a_2}^{\prime }\right|\cos \left(\theta +270°\right)}$

${\displaystyle =\left|a_1\right|\left|{a_2}^{\prime }\right|\cos \left(\theta +360°-90°\right)}$

${\displaystyle =\left|a_1\right|\left|{a_2}^{\prime }\right|\cos \left(\theta -90°\right)}$

${\displaystyle =\left|a_1\right|\left|{a_2}^{\prime }\right|\sin \theta }$

${\displaystyle =\left|a_1\right|\left(\left|a_2\right|\sin \theta \right)}$　･･････(2)

(1)，(2)より，いずれの場合も

${\displaystyle a_1\cdot a_2=\left|a_1\right|\left(\left|a_2\right|\sin \theta \right)}$

となる．

${\displaystyle \left|a_1\right|\left(\left|a_2\right|\sin \theta \right)}$ の絶対値は ${\displaystyle a_1}$と${\displaystyle a_2}$ を2辺とする平行四辺形の面積の値に等しい．

すなわち${\displaystyle \left|\begin{array}{cc}a& c\\ b& d\end{array}\right|}$ の絶対値は${\displaystyle a_1}$と${\displaystyle a_2}$を2辺とする平行四辺形の面積の値に等しい．

${\displaystyle \left|\begin{array}{cc}a& c\\ b& d\end{array}\right|}$の符号は

${\displaystyle 0°\le \theta \le 180°\Rightarrow \left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|\ge 0}$ ，${\displaystyle -180°\le \theta <0°\Rightarrow \left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|<0}$

となる．

　

ホーム>>カテゴリー分類>>行列>>線形代数>>行列式の幾何学的解釈

最終更新日： 2023年6月12日