単射・全射・全単射

写像の仕方によって，単射・全射・全単射という言い方がある．

■単射

写像${\displaystyle f:X\to Y}$において，集合 ${\displaystyle X}$の要素は必ず異なる集合${\displaystyle Y}$の要素と対応している場合を単射(injection)という．

言い換えると

${\displaystyle x_1,x_2\in X}$，${\displaystyle y_1=f\left(x_1\right),y_2=f\left(x_2\right)\in Y}$において， ${\displaystyle x_1\ne x_2\Rightarrow y_1\ne y_2}$

となる．（ここを参照）

■全射

写像${\displaystyle f:X\to Y}$において，集合 ${\displaystyle Y}$の要素は必ず集合${\displaystyle X}$の要素と対応付けられている場合を全射(surjection)という．

言い換えると

${\displaystyle f\left(X\right)=Y}$ ，ただし${\displaystyle f\left(X\right)=\left\{f\left(x\right)\left|x\in X\right.\right\}}$

となる．

■全単射

全射でかつ単射の場合を全単射(bijection)という．

■各写像のイメージ図

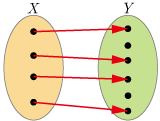
• 単射

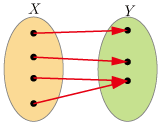
• 全射

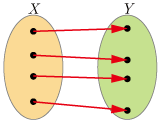
• 全単射

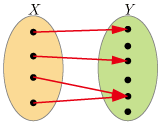
• 単射でも全射でもない

ホーム>>カテゴリー分類>>行列>>線形代数>>単射・全射・全単射

最終更新日：2022年9月3日