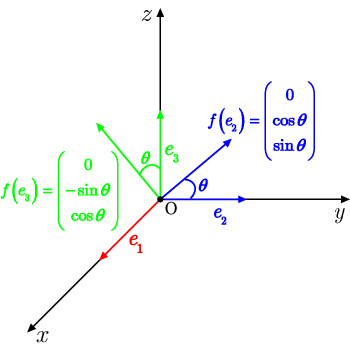3次元の回転行列(x軸まわり)
点
を
軸のまわりに
回転して点
に移す一次変換の表現行列は
である.
軸の正方向に右ねじを向け,
軸の正方向に右ねじが進む回転方向を正方向とする.
■導出
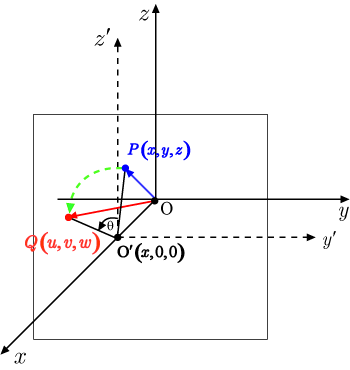
軸の回転では
成分の値は変化しないので
……(1)
となる.よって,点
から点へ移す変換は,
平面に平行で
軸と
軸の値が
で交わる平面上の点
を中心として
回転したものと考えることができる.
したがって
……(2)
……(3)
となる.
(1),(2),(3)より
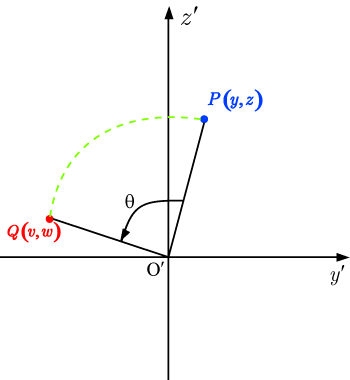
となる.
以上より,
軸のまわりに
回転する一次変換の表現行列は
である.
■別の方法
軸のまわりに
回転する一次変換をとする.
次元ベクトル空間の基本ベクトルを
,
,
とすると
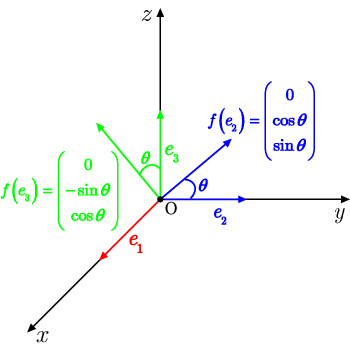
よって,表現行列は
となる.
ホーム>>カテゴリー分類>>行列>>線形代数>>列ベクトル
最終更新日:
2025年1月17日