関連するページを見るにはこのグラフ図を利用してください．

組合せの総数

組合せとはいくつかあるものの中からある個数とりだしたもので，取り出した順序や並べ方に関係しない組みのことである．

異なる$n$個のものから$r$個とった組合せの総数は

${\displaystyle {}_{n}C_r}$ 

と表し，異なる$n$個のものから$r$個とった順列の総数を異なる $r$個のものから$r$個とった順列の総数で割った値となる．すなわち

${\displaystyle {\displaystyle {}_{n}C_r=\frac{{}_{n}P_r}{{}_r{P}_r}}}$ ${\displaystyle =\frac{n\left(n-1\right)\cdot \cdot \cdot \cdot \cdot \cdot \left(n-r+1\right)}{r!}}$${\displaystyle =\frac{n!}{r!\left(n-r\right)!}}$

となる．

■事例による説明

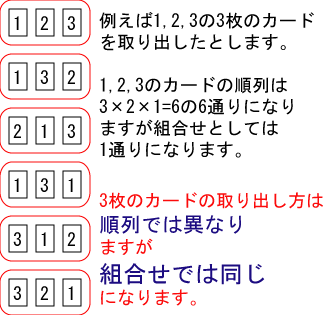1，2，3，4，5の数字をそれぞれ書いたカードが5枚あります．カード5枚の中から3枚カードを取り出す組合せの総数はいくつあるか．

この場合は ${\displaystyle n=5}$ に相当する．

3枚カードを取り出す順列の総数から3枚のカードを並べる順列の総数を割ったものが組合せの総数になる．

${\displaystyle {}_5{}^{}C{}_3^{}=\frac{{}_5{P}_3}{{}_3{P}_3}}$

${\displaystyle =\frac{5\times \left(5-1\right)\times \left(5-2\right)}{3\times \left(3-1\right)\times \left(3-2\right)}}$

${\displaystyle =\frac{5\times 4\times 3}{3\times 2\times 1}}$

${\displaystyle =10}$

よって，10通りになる．

 

 

ホーム>>カテゴリー分類>>確率>>個数の処理：組合せの総数

最終更新日： 2024年2月9日

[ページトップ]

利用規約

google translate (English version)