関連するページを見るにはこのグラフ図を利用してください．

二項定理

${\displaystyle {\left(a+b\right)}^n}$${\displaystyle ={}_n{C}_0{a}^n+{}_n{C}_1{a}^{n-1}b}$${\displaystyle +{}_n{C}_2{a}^{n-2}{b}^2}$${\displaystyle +\cdots \cdots +{}_n{C}_r{a}^{n-r}{b}^r}$${\displaystyle +\cdots \cdots +{}_n{C}_n{b}^n}$

${\displaystyle =\sum _{r=0}^n{}_n{C}_r{a}^{n-r}{b}^r}$

一般項：　${\displaystyle {}_n{C}_r{a}^{n-r}{b}^r\left(r=0,1,2,\cdots \cdots ,n\right)}$

二項係数：${\displaystyle {}_n{C}_r=\frac{n!}{r!\left(n-r\right)!}}$${\displaystyle =\frac{n\left(n-1\right)\left(n-2\right)\cdots \left(n-r+1\right)}{r!}}$

${\displaystyle {}_n{C}_r={}_{n-1}{C}_{r-1}+{}_{n-1}{C}_r\left(n\ge 2\right),}$${\displaystyle {}_n{C}_r={}_n{C}_{n-r}}$

特に，${\displaystyle {}_n{C}_0={}_n{C}_n=1}$

■二項定理の導出

${\displaystyle {\left(a+b\right)}^n}$ の二項展開を${\displaystyle n=1}$ から順に計算してみる．

${\displaystyle {\left(a+b\right)}^1=1·a+1·b}$

${\displaystyle {\left(a+b\right)}^2=\left(a+b\right)\left(a+b\right)}$

${\displaystyle =\left(a+b\right)a+\left(a+b\right)b}$

${\displaystyle =aa+ba+ab+bb}$（単項式の数は${\displaystyle 2\times 2=4}$ ）

${\displaystyle =\mathbf{1}·a^2+\mathbf{1}·ab+\mathbf{1}·ab+\mathbf{1}·b^2}$

${\displaystyle =\mathbf{1}·a^2+\left(\mathbf{1}+\mathbf{1}\right)ab+1·b^2}$

${\displaystyle =\mathbf{1}·a^2+\mathbf{2}·ab+\mathbf{1}·b^2}$

以上4乗まで計算した．これらから，${\displaystyle {\left(a+b\right)}^n}$ を展開すると単項式は ${\displaystyle 2^n}$ でき，${\displaystyle a^{n-r}{b}^r}$ の単項式は ${\displaystyle a}$ と${\displaystyle b}$ から成る${\displaystyle n}$個の文字列中から${\displaystyle b}$の文字が入る位置を ${\displaystyle r}$個選ぶ組合せに等しいことが推測できる． よって，

${\displaystyle {\left(a+b\right)}^n=\sum _{r=0}^n{}_n{C}_r{a}^{n-r}{b}^r}$　･･････(1)

となることがわかる．これを数学的帰納法を用いて証明する．

${\displaystyle n=1}$ のとき，

${\displaystyle {\left(a+b\right)}^1{=}_1{C}_0{a}^1{b}^0{+}_1{C}_1{a}^0{b}^1=a+b}$

となり，(1)は成り立つ．

${\displaystyle n=k}$のとき，(1)が成りたつと仮定すると，すなわち

${\displaystyle {\left(a+b\right)}^k=\sum _{r=0}^k{}_k{C}_r{a}^{k-r}{b}^r}$

が成り立つと仮定する．

${\displaystyle {\left(a+b\right)}^{k+1}=\left(a+b\right){\left(a+b\right)}^k}$

${\displaystyle =\left(a+b\right)\sum _{r=0}^k{}_k{C}_r{a}^{k-r}{b}^r}$

${\displaystyle =\sum _{r=0}^k{}_k{C}_{r}a·a^{k-r}{b}^r+\sum _{r=0}^k{}_k{C}_r{a}^{k-r}b·b^r}$

${\displaystyle =\sum _{r=0}^k{}_k{C}_r{a}^{k-r+1}{b}^r+\sum _{r=0}^k{}_k{C}_r{a}^{k-r}{b}^{r+1}}$

第2項の${\displaystyle {\displaystyle \sum _{r=0}^k{}_k{C}_r{a}^{k-r}{b}^{r+1}}}$において${\displaystyle {\displaystyle r+1=s}}$，${\displaystyle {\displaystyle r=s-1}}$として，式を書き換えると

${\displaystyle =\sum _{r=0}^k{}_k{C}_r{a}^{k-r+1}{b}^r}$${\displaystyle +\sum _{s=1}^{k+1}{}_k{C}_{s-1}{a}^{k-(s-1)}{b}^s}$

第2項の${\displaystyle s}$ を${\displaystyle r}$ に書き換えて，式を少し変形すると，

${\displaystyle =\sum _{r=0}^k{}_k{C}_r{a}^{\left(k+1\right)-r}{b}^r}$${\displaystyle +\sum _{r=1}^{k+1}{}_k{C}_{r-1}{a}^{\left(k+1\right)-r}{b}^r}$

${\displaystyle ={}_k{C}_0{a}^{k+1}+\sum _{r=1}^k{}_k{C}_r{a}^{\left(k+1\right)-r}{b}^r}$${\displaystyle +\sum _{r=1}^k{}_k{C}_{r-1}{a}^{\left(k+1\right)-r}{b}^r+{}_{k+1}{C}_{k+1}{b}^{k+1}}$

ここで

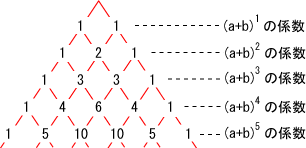
より （この関係からパスカルの三角形が得られる）

${\displaystyle ={}_k{C}_0{a}^{k+1}+\sum _{r=1}^k{}_{k+1}{C}_r{a}^{\left(k+1\right)-r}{b}^r}$${\displaystyle +{}_{k+1}{C}_{k+1}{b}^{k+1}}$

${\displaystyle =\sum _{r=0}^{k+1}{}_{k+1}{C}_r{a}^{\left(k+1\right)-r}{b}^r}$

よって，${\displaystyle n=k+1}$ のときも(1)が成り立ち，数学的帰納法により，(1)はすべての自然数${\displaystyle a}$  に対して成り立つ．

${\displaystyle {\left(a+b\right)}^n}$ の係数は，上述した具体的な計算事例と${\displaystyle {}_k{C}_r+{}_k{C}_{r-1}={}_{k+1}{C}_r}$ の関係から，パスカルの三角形が得られる．

パスカルの三角形を下に示す．

　

ホーム>>カテゴリー分類>>数列>>二項定理

最終更新日： 2023年7月27日

[ページトップ]

利用規約

google translate (English version)