関連するページを見るにはこのグラフ図を利用してください．

平均

いま，${\displaystyle n}$ 個のデータの値が ${\displaystyle x_1,x_2,\cdots ,x_n}$ とあるとき，その平均 ${\displaystyle \overline{x}}$ は

${\displaystyle \overline{x}=\frac{1}{n}\left(x_1+x_2+\cdots +x_n\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n{x}_i}}$ 　

で定義される．(和記号Σ参照）

取り扱うデータが確率変数$X$である場合，平均を$E\left(X\right)$という表現を用いて

${\displaystyle E\left(X\right)=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{x}_i}$

定義される．この平均のことを期待値ともいう．$E\left(X\right)$の$E$はExpected Value(期待値)の頭文字である．

確率関数 $f\left(x\right)$ を用いると

• 離散型確率変数の場合：${\displaystyle E\left(X\right)={\displaystyle \sum _{i=1}^n{x}_{i}f\left(x_i\right)}}$
• 連続型確率変数の場合：${\displaystyle E\left(X\right)={\displaystyle {\int }_{-\infty }^{\infty }xf\left(x\right)dx}}$

■例

10個のデータ

${\displaystyle 5}$,${\displaystyle 7}$,${\displaystyle 11}$,${\displaystyle 4}$,${\displaystyle 8}$,${\displaystyle 15}$,${\displaystyle 9}$,${\displaystyle 8}$,${\displaystyle 10}$,${\displaystyle 11}$

の平均 ${\displaystyle \overline{x}}$ は

${\displaystyle =8.8}$

となる．

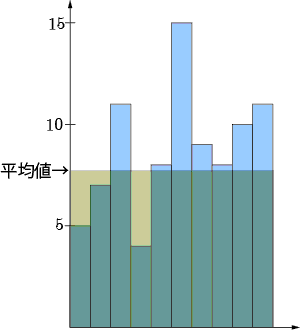個々のデータを幅が１で高さがデータ値となる長方形を図のように横に並べると，平均は10個の長方形の面積の和と同じ面積になる幅が10の長方形の高さになる．

　

ホーム>>カテゴリー分類>>確率>>確率統計>>平均

　最終更新日： 2024年2月9日

[ページトップ]

利用規約

google translate (English version)