関連するページを見るにはこのグラフ図を利用してください．

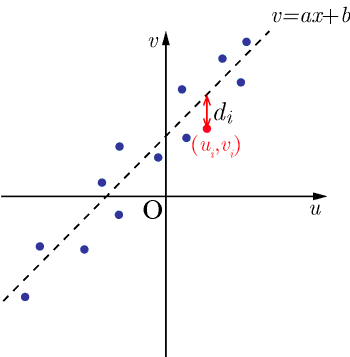
相関係数の式の導出

変量 $x$ ， $y$ の相関係数は

${\displaystyle r=\frac{{\sigma }_{xy}}{{\sigma }_x{\sigma }_y}}$

${\displaystyle {\sigma }_{xy}=\frac{1}{n}\sum _{i=1}^n\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}$ （ $x$ ， $y$ の共分散）

${\displaystyle {\sigma }_x=\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(x_i-\overline{x}\right)}^2}}$ （ $x$ の標準偏差）

${\displaystyle {\sigma }_y=\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(x_i-\overline{x}\right)}^2}}$ （ $y$ の標準偏差）

である．

■相関係数の式の導出

2種類の変量の間の関係を示す相関図において，点がある直線の近くに集まるとき，2種類の変量の間には相関があるという．

2種類の変量 $x$ と $y$ を標準化した

${\displaystyle u_i=\frac{x_i-\overline{x}}{{\sigma }_x}}$ ， ${\displaystyle v_i=\frac{y_i-\overline{y}}{{\sigma }_y}}$

の相関の程度を以下のようにして調べることにする．標準化するのは数式の取り扱いを簡単なするためである．2種類の変量 ${\displaystyle u_i}$ , ${\displaystyle v_i}$ の相関図の点は， ${\displaystyle v=au+b}$ で表される直線の近くに集まる傾向があると仮定する．この直線と，実際の変量との差の2乗和 ${\displaystyle {\Delta }^2}$

${\displaystyle {\Delta }^2={\displaystyle \sum _{i=1}^n{d}_i^2}={\displaystyle \sum _{i=1}^n{\left\{v_i-\left(a{u}_i+b\right)\right\}}^2}}$

を計算してみる．(参考：最小ニ乗法)

${\displaystyle {\Delta }^2}$ の値が大きいと多くの変量が直線から離れており相関が弱く， ${\displaystyle {\Delta }^2}$ の値が小さいと変量が直線の近くに集まっており相関が強いと判断できる．

${\displaystyle {\Delta }^2={\displaystyle \sum _{i=1}^n{d}_i^2}={\displaystyle \sum _{i=1}^n{\left\{v_i-\left(a{u}_i+b\right)\right\}}^2}}$

${\displaystyle ={\displaystyle \sum _{i=1}^n\left\{v_i^2-2v_i\left(a{u}_i+b\right)+{\left(a{u}_i+b\right)}^2\right\}}}$

${\displaystyle ={\displaystyle \sum _{i=1}^n\left(v_i^2-2u_i{v}_{i}a-2v_{i}b+u_i^2{a}^2+2u_{i}ab+b^2\right)}}$

${\displaystyle ={\displaystyle \sum _{i=1}^n{v}_i^2}-2\left({\displaystyle \sum _{i=1}^n{u}_i{v}_i}\right)a-2\left({\displaystyle \sum _{i=1}^n{v}_i}\right)b}$ ${\displaystyle +\left({\displaystyle \sum _{i=1}^n{u}_i^2}\right)a^2}$ ${\displaystyle +2\left({\displaystyle \sum _{i=1}^n{u}_i}\right)ab}$ ${\displaystyle +\left({\displaystyle \sum _{i=1}^{n}1}\right)b^2}$

${\displaystyle =n-2\left({\displaystyle \sum _{i=1}^n{u}_i{v}_i}\right)a-0+n{a}^2+0+n{b}^2}$

∵　 ${\displaystyle {\displaystyle \sum }_{i=1}^n{u}_i=0}$ ， ${\displaystyle {\displaystyle \sum }_{i=1}^n{v}_i=0}$ ， ${\displaystyle {\displaystyle \sum }_{i=1}^n{u}_i^2=1}$ ， ${\displaystyle {\displaystyle \sum }_{i=1}^n{v}_i^2=1}$

${\displaystyle =n{a}^2-2\left({\displaystyle \sum }_{i=1}^n{u}_i{v}_i\right)a+n{b}^2+n}$

${\displaystyle a}$ と ${\displaystyle b}$ の2次関数となっている．この関数を ${\displaystyle a}$ , ${\displaystyle b}$ の順に平方完成する．

${\displaystyle =n{\left\{a-\frac{1}{n}{\displaystyle \sum _{i=1}^n{u}_i{v}_i}\right\}}^2+n{b}^2+n-\frac{1}{n}{\left({\displaystyle \sum _{i=1}^n{u}_i{v}_i}\right)}^2}$

${\displaystyle =n{\left\{a-\frac{1}{n}{\displaystyle \sum _{i=1}^n{u}_i{v}_i}\right\}}^2+n{b}^2}$ ${\displaystyle +n\left\{1-{\left(\frac{1}{n}{\displaystyle \sum _{i=1}^n{u}_i{v}_i}\right)}^2\right\}}$

${\displaystyle {\Delta }^2}$ は

${\displaystyle a=\frac{1}{n}{\displaystyle \sum _{i=1}^n{u}_i{v}_i}}$ ， ${\displaystyle b=0}$

のとき最小となり，最小値 ${\displaystyle {\Delta }_{\min }^2}$ は

${\displaystyle n\left\{1-{\left(\frac{1}{n}{\displaystyle \sum _{i=1}^n{u}_i{v}_i}\right)}^2\right\}}$

となる．

この時，原点を通る直線 ${\displaystyle v=\left(\frac{1}{n}{\displaystyle \sum _{i=1}^n{u}_i{v}_i}\right)u}$ の回りに最も集まっているといえる．

最小値は， ${\displaystyle \frac{1}{n}{\displaystyle \sum _{i=1}^n{u}_i{v}_i}}$ の値に依存しており， ${\displaystyle \frac{1}{n}{\displaystyle \sum _{i=1}^n{u}_i{v}_i}=\pm 1}$ のとき，最小値は ${\displaystyle 0}$ となり，すべての変量が直線 ${\displaystyle v=\left(\frac{1}{n}{\displaystyle \sum _{i=1}^n{u}_i{v}_i}\right)u}$ 上に存在することになる．

この ${\displaystyle \frac{1}{n}{\displaystyle \sum _{i=1}^n{u}_i{v}_i}}$ の値を相関係数 $r$ と定義している．この相関係数を， $x$ ， $y$ を使って表すと

${\displaystyle r=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{u}_i{v}_i}$ ${\displaystyle =\frac{1}{n}{\displaystyle \sum }_{i=1}^n\frac{x_i-\overline{x}}{{\sigma }_x}\cdot \frac{y_i-\overline{y}}{{\sigma }_y}}$ ${\displaystyle =\frac{{\displaystyle \frac{1}{n}{\displaystyle \sum }_{i=1}^n\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}}{{\sigma }_x{\sigma }_y}}$ ${\displaystyle =\frac{{\sigma }_{xy}}{{\sigma }_x{\sigma }_y}}$

ここで， ${\displaystyle \frac{1}{n}{\displaystyle \sum }_{i=1}^n\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)={\sigma }_{xy}}$ 共分散と定義している．

となり冒頭の式になる．

●最小値 ${\displaystyle {\Delta }_{\min }^2}$ について考えてみる

${\displaystyle {\Delta }^2\geqq 0}$ より

${\displaystyle n\left\{1-{\left(\frac{1}{n}{\displaystyle \sum _{i=1}^n{u}_i{v}_i}\right)}^2\right\}\geqq 0}$

${\displaystyle n\left\{{\left(\frac{1}{n}{\displaystyle \sum _{i=1}^n{u}_i{v}_i}\right)}^2-1\right\}\leqq 0}$

${\displaystyle n\left\{\left(\frac{1}{n}{\displaystyle \sum _{i=1}^n{u}_i{v}_i}\right)-1\right\}\left\{\left(\frac{1}{n}{\displaystyle \sum _{i=1}^n{u}_i{v}_i}\right)+1\right\}\leqq 0}$

よって

${\displaystyle -1\leqq \frac{1}{n}{\displaystyle \sum _{i=1}^n{u}_i{v}_i}\leqq 1}$ ⇒　 ${\displaystyle -1\leqq r\leqq 1}$

${\displaystyle {\Delta }_{\min }^2}$ の最大値は ${\displaystyle n}$ で最小値は ${\displaystyle 0}$ となる．

　

ホーム>>カテゴリー分類>>確率統計>>相関係数

最終更新日： 2025年2月5日

[ページトップ]

利用規約

google translate (English version)