|
|||||||||||||
|
|||||||||||||
|
関連するページを見るにはこのグラフ図を利用してください．
判別式
2次方程式 ax2+bx+c=0 (a≠0) において
D=b2−4ac
を判別式といい．この D の値で2次方程式の解の個数を判定する．
| D の値 | 解の個数 |
| D ＞0 | 異なる2つの解 |
| D ＝0 | 1つの解（重解） |
| D ＜0 | 解なし（実数解なし） |
b2−4ac は下に示す解の公式の青色の部分にある．
x=−b±√b2−4ac2a
D の値によって2次方程式の解の数が変わる．
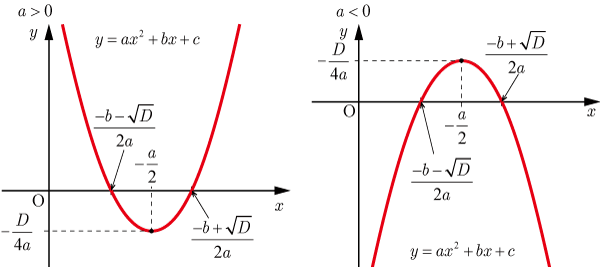
[1] D ＞0 の場合
解は，
x=−b+√D2a , −b−√D2a
で異なる2つの解を持つ．
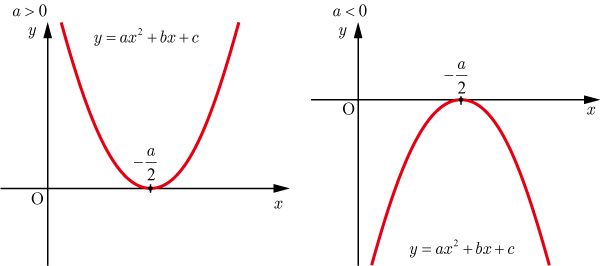
[2] D ＝0の場合
解は，
x=−b2a
で1つの解をもつ．
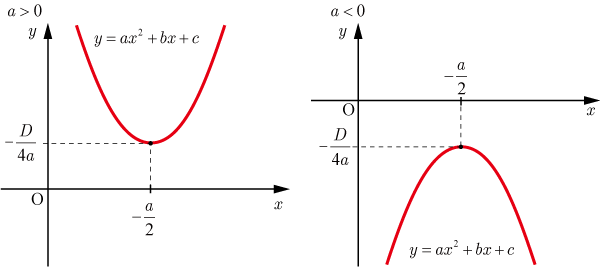
[3] D ＜0の場合
解の公式のルートの中が負となり解（実数解）を持たない ．
最終更新日： 2023年7月26日
