3次関数のグラフ
3次関数を表す一般式は
・・・・・・(1)
である.
⇒
軸との交差の仕方による分類
⇒導関数の判別式による分類
■3次関数のグラフ
下のグラフは(1)の3次関数のグラフを描いたものである.3次関数の係数
,
,
,
を右上のスライダー用いて変化させるとグラフが変化する.
■
軸との交差の仕方による分類
3次関数のグラフは少なくとも
軸と1点で交差する.その交差点を
とすると3次関数は
・・・・・・(2)
と表される.3次関数の特徴を
の判別式の値で分類する.
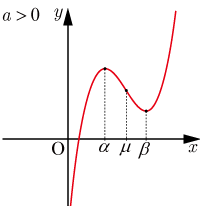
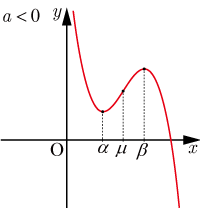
●
,異なる実数解
,
(ただし,
,
)を持つ場合
3次関数は
軸と3点
,
,
で交差する.(2)は以下のようになる.
・・・・・・(3)
,
,
,
は定数.
ただし,
,
,
,
●
,重解
を持つ場合
-
のとき
軸と点
で交差し,点
で接する.(2)は以下のようになる.
・・・・・・(4)
,
,
は定数.
ただし,
,
(4)の導関数を求める.
・・・・・・(5)
したがって,
で
,
より,点
で
軸と接する.
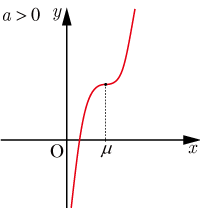
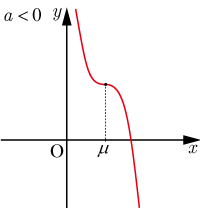
-
のとき
軸と点
で交差するが,点
における接線の傾きはゼロになっている.(2)は以下のようになる.
・・・・・・(6)
,
は定数.
ただし,
(6)の導関数,第2次導関数を求める.
・・・・・・(7)
・・・・・・(8)
したがって,
で
,
,
より,点
は変曲点で
軸と点
で交差するが,点
における接線の傾きはゼロになっている.
●
,実数解を持たない場合
軸と点
で交差する.(2)は以下のようになる.
・・・・・・(6)
,
,
,
は定数.
ただし,
下のグラフは以下の3つの関数のグラフを描いたものである.3次関数の係数
,
,
,
を右上のスライダー用いて変化させるとグラフが変化する.
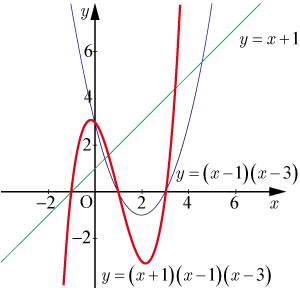
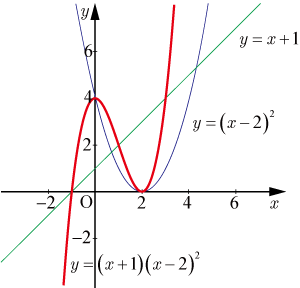
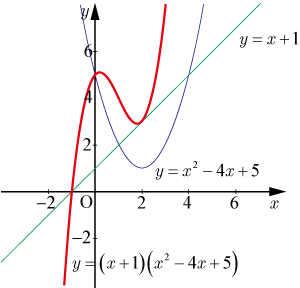
緑線:
・・・・・・(7)
青線:
・・・・・・(8)
赤線:
・・・・・・(9)
JSXGraph Copyright (C) see http://jsxgraph.org
■導関数の判別式による分類
導関数の判別式
で3次関数グラフの特徴を分類する.
●
,導関数が異なる実数解
,
を持つ場合:
で極値を持つ.点
は変曲点.
◆
,
とすると増減表は以下のようになる.
◆
,
とすると増減表は以下のようになる.
●
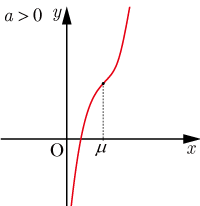
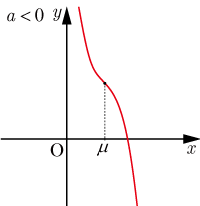
,導関数が重解
を持つ場合:
極値を持たない.点
は変曲点.
◆
とすると増減表は以下のようになる.
◆
とすると増減表は以下のようになる.
●
,導関数が実数解を持たない場合
極値を持たない.点
は変曲点.
◆
とすると増減表は以下のようになる.
◆
とすると増減表は以下のようになる.
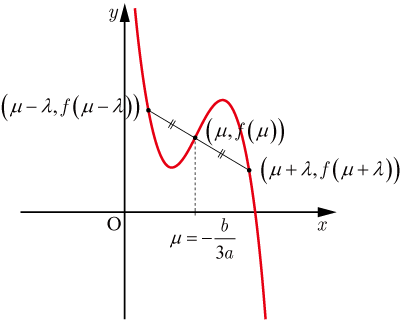
■点対称のグラフ
のグラフは,
変曲点
に関して対称(点対称)である.⇒証明
ホーム>>カテゴリー別分類>>関数>>3次関数
最終更新日:
2025年4月27日