合成関数

2つの関数 $f (x)$ $f (x)$ と $g (x)$ $g (x)$ がある．そして， $f (x)$ $f (x)$ の値域が $g (x)$ $g (x)$ の定義域に含まれているとする．

変数 $x$ $x$ は関数 $f (x)$ $f (x)$ によって $y$ $y$ に対応すると

$y = f (x)$ $y = f (x)$ ･･････(1)

と表される．

今度は， $y$ $y$ を変数と考える．この変数 $y$ $y$ は関数 $g (y)$ $g (y)$ によって $z$ $z$ に対応すると（変数が $x$ $x$ から $y$ $y$ にかえているので $g (y)$ $g (y)$ と表していることに注意すること）

$z = g (y)$ $z = g (y)$ ･･････(2)

と表される．

(2)の変数 $y$ $y$ のかわりに(1)より $f (x)$ $f (x)$ を用いると

$z = g (f (x))$ $z = g (f (x))$

と表される．すなわち，変数 $x$ $x$ は関数 $f$ $f$ につづいて関数 $g$ $g$ を機能させることにより $z$ $z$ に対応する．よって $g (f (x))$ $g (f (x))$ を1つの関数とみなせる．この関数を合成関数といい，

$(g \circ f) (x)$ $(g \circ f) (x)$

と表す．

この合成関数の概念を図で表すと下図のようになる．

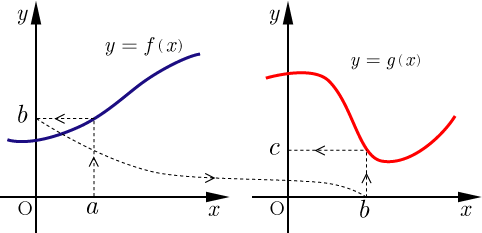
$\begin{array}{l} b = f (a) \\ c = g (b) \end{array}} \Rightarrow c = g (f (a))$ ，あるいは， $(g \circ f) (a)$

合成写像を参照のこと

最終更新日 2023年4月18日