|
|||||||||||||
|
|||||||||||||
|
関連するページを見るにはこの知識グラフを利用してください.
問題リスト←このページに関連している問題です
方程式の実数解の存在定理
関数 が閉区間 において連続で,かつ, ならば,開区間 に方程式 の実数解が少なくとも1つの存在する.
■解説
中間値の定理において, のときに相当する.
ならば, と の符号が異なり,関数 が閉区間 において連続であると, のグラフは少なくとも1箇所 軸と交差することになる.その交点座標の の値が方程式 の実数解となる.以上の内容を以下に図で示す.
● , の場合
-
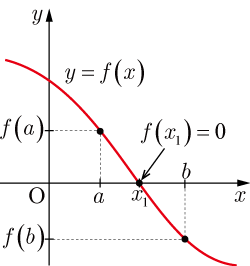
図1 解が の1つ -
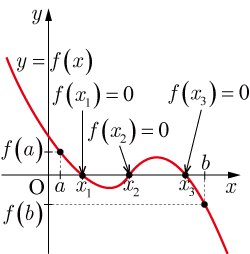
図2 解が , , の3つ
● , の場合
-
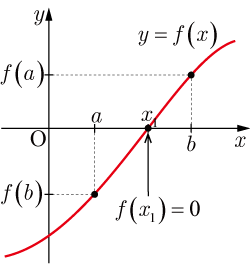
図3 解が の1つ -
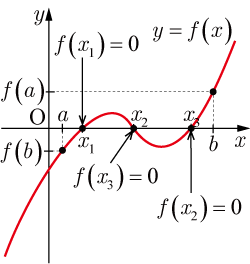
図4 解が , , の3つ
ホーム>>カテゴリー分類>>関数>>方程式の実数解の存在定理
最終更新日: 2025年4月25日