関連するページを見るにはこのグラフ図を利用してください．

漸近線

漸近線とは，曲線の中心部から遠くに離れるほど曲線との距離が限りなく0に近づき，その曲線とは交わる(接触)しない直線のことである．

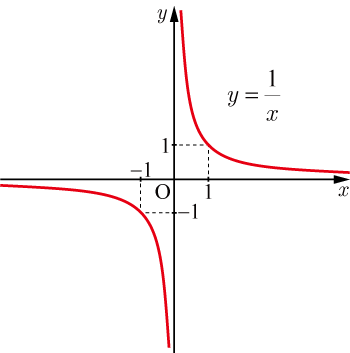
分かりやすい例でいうと，反比例のグラフである．

${\displaystyle y=\frac{1}{x}}$のグラフを見てみると，原点から遠く離れている部分では${\displaystyle x}$軸と${\displaystyle y}$軸に近づいているが，決して交わることはない．

よって，${\displaystyle x}$軸と${\displaystyle y}$軸が漸近線になる．

$y=f\left(x\right)$のグラフに関して，${\displaystyle y}$軸に平行な漸近線の場合

${\displaystyle \underset{x\to a+0}{\lim }f(x)=\infty }$

${\displaystyle \underset{x\to a+0}{\lim }f(x)=-\infty }$

${\displaystyle \underset{x\to a-0}{\lim }f(x)=\infty }$

${\displaystyle \underset{x\to a-0}{\lim }f(x)=-\infty }$

（関数の極限の右側極限、左側極限を参照）

のどれか1つでも成り立てば， ${\displaystyle x=a}$が漸近線となる．

${\displaystyle x}$軸に平行な漸近線の場合

${\displaystyle \underset{x\to +\infty }{\lim }f\left(x\right)=a}$

${\displaystyle \underset{x\to -\infty }{\lim }f\left(x\right)=a}$

のどれか1つでも成り立てば， ${\displaystyle y=a}$が漸近線となる．

 

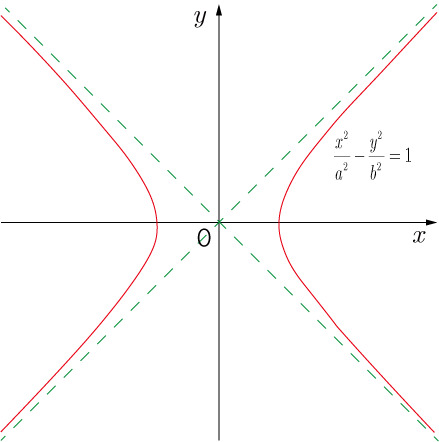また，双曲線 ${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=1}$ のグラフのように1次関数が漸近線になることもある．

関数この場合，${\displaystyle y=\pm \frac{b}{a}x}$が漸近線である．

関数${\displaystyle f\left(x\right)}$ の漸近線が1次関数 ${\displaystyle y=ax+b}$の場合

傾き${\displaystyle a}$: ${\displaystyle a=\underset{x\to \pm \infty }{\lim }\frac{f\left(x\right)}{x}}$

$y$切片${\displaystyle b}$: ${\displaystyle b=\underset{x\to \pm \infty }{\lim }\left\{f\left(x\right)-ax\right\}}$

となる．

 

 

 

ホーム>>カテゴリー別分類>>関数>>漸近線

最終更新日： 2024年3月1日

[ページトップ]

利用規約

google translate (English version)