関連するページを見るにはこのグラフ図を利用してください．

曲率半径 (curvature and radius of curvature)

曲率 (curvature) は，曲線上のある点におけるその曲線の曲がり具合を示す指標であり，その曲率の逆数が 曲率半径 (radius of curvature) を表す．曲線上の任意の点付近の曲線の微小部分は，その点での曲率半径を半径とする円（曲率円(curvature circle)という）で近似できる．曲率半径が大きいと曲がり具合が緩く，曲率半径が小さいと曲がり具合がきつくなる．したがって，曲がり具合がきついほど曲率は大きくなる．

■ 曲率半径の定義

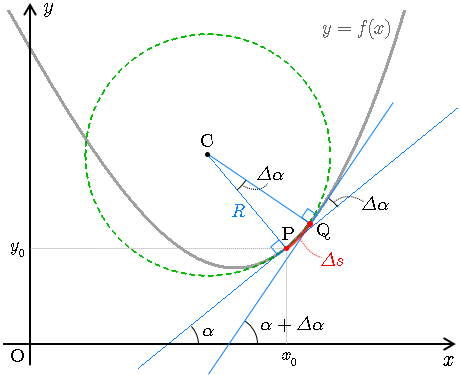
${\displaystyle xy}$ 平面で定義された曲線 ${\displaystyle y=f(x)}$ 上の点 P ${\displaystyle (x_0,y_0)}$ から曲線に沿って ${\displaystyle \Delta s}$ だけ変位した点を Q とする．この ${\displaystyle \Delta s}$ 部分を円弧とみなし，その円の中心を点 C ，角PCQを ${\displaystyle \Delta \alpha }$ とすると，この円の半径は

${\displaystyle R=\left|\frac{\Delta s}{\Delta \alpha }\right|}$

である（絶対値をとっているのは角 ${\displaystyle \Delta \alpha }$ が時計回りの場合，負の値となるからである）．ここで，極限 ${\displaystyle \Delta s\to 0}$ をとると，点 P における曲率半径

${\displaystyle R=\underset{\Delta s\to 0}{\lim }\left|\frac{\Delta s}{\Delta \alpha }\right|=\left|\frac{ds}{d\alpha }\right|}$

が求まる．点 P における曲率 ${\displaystyle \kappa }$ は曲率半径 ${\displaystyle R}$ の逆数なので次式となる．

${\displaystyle \kappa =\frac{1}{R}=\left|\frac{d\alpha }{ds}\right|}$

ただし，絶対値をとらずに曲率を定義する場合もあり（符号付き曲率 (signed curvature) ），曲率の値は正にも負にもなる．この場合，その符号は微小角度 ${\displaystyle d\alpha }$ の向きを表し，正のとき反時計回りの向き，負のとき時計回りの向きを示す．

■ 曲線 ${\displaystyle y=f(x)}$ の曲率半径

図に示すように，点 P での接線と ${\displaystyle x}$ 軸とのなす角を ${\displaystyle \alpha }$ とすると，点 Q での接線と ${\displaystyle x}$ 軸とのなす角は ${\displaystyle \alpha +\Delta \alpha }$ となるので，角PCQは点 P から点 Q の接線の角度の増分に対応する．点 P での接線の傾きは

${\displaystyle \tan \alpha =\frac{dy}{dx}}$

なので，

${\displaystyle (\tan \alpha {)}^{\prime }d\alpha ={\left(\frac{dy}{dx}\right)}^{\prime }dx}$     ⇒     ${\displaystyle \frac{d\alpha }{{\cos }^2\alpha }=\frac{d^{2}y}{d{x}^2}dx}$     ⇒     ${\displaystyle d\alpha ={\cos }^2\alpha \frac{d^{2}y}{d{x}^2}dx}$ ${\displaystyle =\frac{1}{1+{\tan }^2\alpha }\frac{d^{2}y}{d{x}^2}dx}$

となり，最終的に

${\displaystyle d\alpha =\frac{\frac{d^{2}y}{d{x}^2}}{1+{\left(\frac{dy}{dx}\right)}^2}dx}$

を得る．また，

${\displaystyle ds=\sqrt{{(dx)}^2+{(dy)}^2}}$ ${\displaystyle =\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}$

であるので，曲率半径 ${\displaystyle R}$ は ${\displaystyle x}$ の関数として

${\displaystyle R(x)=\left|\frac{ds}{d\alpha }\right|}$ ${\displaystyle =\left|\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}\cdot \frac{1+{\left(\frac{dy}{dx}\right)}^2}{\frac{d^{2}y}{d{x}^2}}\right|}$ ${\displaystyle =\frac{{\left\{1+{\left(\frac{dy}{dx}\right)}^2\right\}}^{\frac{3}{2}}}{\left|\frac{d^{2}y}{d{x}^2}\right|}}$

と求まる．点 P では ${\displaystyle x=x_0}$ なので，点 P における曲率半径は ${\displaystyle R(x_0)}$ である．

また，曲率中心 (center of curvature)（点 P 付近の曲線を近似する円の中心）C の座標 ${\displaystyle (c_x,c_y)}$ は次式で求まる．

${\displaystyle (c_x,c_y)=(x_0,y_0)+\frac{ds}{d\alpha }\left(-\frac{dy}{ds},\frac{dx}{ds}\right)}$ ${\displaystyle =(x_0,y_0)+\left(-\frac{dy}{d\alpha },\frac{dx}{d\alpha }\right)}$ ${\displaystyle =(x_0,y_0)+\frac{1+{\left(\frac{dy}{dx}\right)}^2}{\frac{d^{2}y}{d{x}^2}}\left(-\frac{dy}{dx},1\right)}$

■ パラメータ表示された曲線 ${\displaystyle x=x(t)}$ , ${\displaystyle y=y(t)}$ の曲率半径(導出)

■ 陰関数表示された曲線 ${\displaystyle F(x,y)=0}$ の曲率半径(導出)

ホーム>>カテゴリー分類>>幾何>>曲率半径

[ページトップ]

利用規約

google translate (English version)