ヘロンの公式

3辺の長さを， $a$ ， $b$ ， $c$ とすると，三角形の面積 $S$ は

$S = \sqrt{s (s - a) (s - b) (s - c)}$

となる．ただし， $s = \frac{a + b + c}{3}$ とする．

●参考

$S = \frac{1}{2} \sqrt{{| \overset{⟶}{AB} |}^{2} \cdot {| \overset{⟶}{AC} |}^{2} - {(\overset{⟶}{AB} \cdot \overset{⟶}{AC})}^{2}}$ ⇒導出

■導出

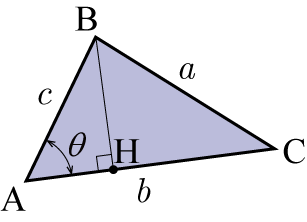
図のような三角形 $ABC$ を考える．線分 $BC$ の長さを $a$ ，線分 $AC$ の長さを $b$ ，線分 $AB$ の長さを $c$ とする．頂点 $B$ から線分 $AC$ に垂線を降ろし線分 $AC$ との交点を $H$ とする．三角形 $ABC$ の底辺を $AA$ とうすると，高さは線分 $BH$ となる．この場合，三角形の面積 $S$ は

$S = \frac{1}{2} b (c \sin θ)$ $= \frac{1}{2} b c \sin θ$ ･･････(1)

（∵ $BH = c \sin θ$ ）

となる．(1)より

$S^{2} = \frac{1}{4} b^{2} c^{2} \sin^{2} θ = \frac{1}{4} b^{2} c^{2} (1 - \cos^{2} θ)$ ･･････(2)

となる．余弦定理より

$a^{2} = b^{2} + c^{2} - 2 b c \cos θ$

$\cos θ = \frac{b^{2} + c^{2} - a^{2}}{2 b c}$ ･･････(3)

(3)を(2)に代入する．

$S^{2} = \frac{1}{4} b^{2} c^{2} \{1 - {(\frac{b^{2} + c^{2} - a^{2}}{2 b c})}^{2}\}$

$= \frac{1}{4} b^{2} c^{2} \{\frac{4 b^{2} c^{2} - {(b^{2} + c^{2} - a^{2})}^{2}}{4 b^{2} c^{2}}\}$

$= \frac{1}{16} \{4 b^{2} c^{2} - {(b^{2} + c^{2} - a^{2})}^{2}\}$

$x^{2} - y^{2} = (x + y) (x - y)$ の関係を用いて式を変形する

$= \frac{1}{16} \{4 b^{2} c^{2} + (b^{2} + c^{2} - a^{2})\} \{4 b^{2} c^{2} - (b^{2} + c^{2} - a^{2})\}$

$= \frac{1}{16} \{2 b c - a^{2} + b^{2} + c^{2}\} \{2 b c + a^{2} - b^{2} - c^{2}\}$

$= \frac{1}{16} \{b^{2} + 2 b c + c^{2} - a^{2}\} \{a^{2} - b^{2} + 2 b c - c^{2}\}$

$= \frac{1}{16} \{{(b + c)}^{2} - a^{2}\} \{a^{2} - {(b - c)}^{2}\}$

$= \frac{1}{16} \{(b + c) + a\} \{(b + c) - a\} \{a + (b - c)\} \{a - (b - c)\}$

$= \frac{1}{16} \{b + c + a\} \{b + c - a\} \{a + b - c\} \{a - b + c\}$

$= (\frac{b + c + a}{2}) (\frac{b + c - a}{2}) (\frac{a + b - c}{2}) (\frac{a - b + c}{2})$

$s = \frac{a + b + c}{3}$ を代入する．

$= (\frac{b + a + c}{2}) (\frac{a + b + c}{2} - a) (\frac{a + b + c}{2} - c) (\frac{a + b + c}{2} - b)$

$= s (s - a) (s - c) (s - b)$

$= s (s - a) (s - b) (s - c)$ ･･････(1)

したがって

$S = \sqrt{s (s - a) (s - b) (s - c)}$

の関係が得られる．

ホーム>>カテゴリー分類>>幾何>>2点間の距離

最終更新日： 2025年10月20日