2次曲線の分類 (Classification of quadratic curves)
, の2次式
, ······ (1)
で表される2次曲線(円錐曲線)は,判別式 (2次形式の対称行列の行列式),離心率 ,円錐切断面の角度などにより分類され,適当な座標変換 (平行移動と直交変換)によって標準形に変換できる(2次曲線の標準化).
| 名称 | 非退化2次曲線 | |||||
|---|---|---|---|---|---|---|
| 楕円 ⇒ 詳細 | 双曲線 ⇒ 詳細 | 放物線 ⇒ 詳細 | ||||
| 定義 | 2つの定点(焦点)からの距離の和が一定である点の軌跡 | 2つの定点(焦点)からの距離の差が一定である点の軌跡 | 1つの定点(焦点)と,この点を通らない直線からの距離が等しい点の軌跡 | |||
| 標準形 |
のときは円 (2つの焦点は重なり1点となる) |
|||||
| 媒介変数 |
媒介変数を とする(右も同じ) |
または |
または |
|
|
|
| 図形 |
(横長)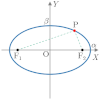
|
(縦長)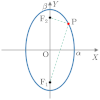
|
横向き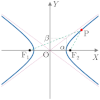
|
縦向き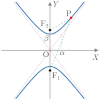
|
横向き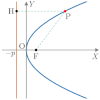
|
縦向き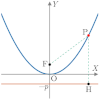
|
| 焦点 | ||||||
| 中心 | 2つの焦点の中点(有心) (2次曲線は中心に関して点対称となる) |
なし(無心) | ||||
| 判別式 |
, , は式(1)の係数 式(1)の左辺に中心の座標を代入した値が負値 |
, , は式(1)の係数 式(1)の左辺に中心の座標を代入した値が 以外 |
, , , , は式(1)の係数 |
|||
| 離心率 | ||||||
| 準線 | ||||||
| 漸近線 | なし | なし | ||||
| 接線 | 2次曲線(標準形)上の点 における接線 | |||||
| 法線 | 2次曲線(標準形)上の点 における法線 | |||||
|
|
|
|||||
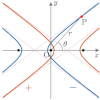
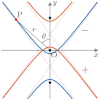
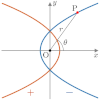
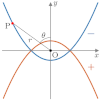
| 極方程式 | 1つの焦点を原点とした表現(楕円・双曲線の場合, でどちらの焦点になるかが決まる) | |||||
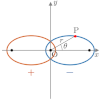
|
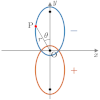
|
|
|
|
|
|
| 円錐切断面 | 円錐切断面は円錐の頂点を通らない(下記の母線とは円錐の頂点から底面の円周上の点までを結ぶ線分のこと) | |||||
対の円錐の片方の母線と交わる平面

|
対の円錐の両方の母線と交わる平面
|
円錐の母線と平行な平面

|
||||
| 退化 | 1つの点 | 交差する2つの直線 | 平行な2つの直線 | |||
| 退化条件 | ||||||
| 上式 は,式(1)の左辺に中心の座標を代入した値が になることと等価 |
上式は,
または
と等価
( なので両式は同等) |
|||||
| 特徴 | 中心の1点のみが式(1)を満たす | 双曲線の2つの焦点を一致させた極限とみなせる(交差する2つの直線は双曲線の2つの漸近線に相当し,交点は中心となる) | 楕円の短径を一定に保ち,長径(焦点間距離)を無限大にしたときの図形,あるいは,双曲線の中心と頂点との間の距離を一定に保ち,焦点間距離を無限大にしたときの図形に対応する.このとき,平行な2直線間の距離はその一定値の2倍となる. | |||
| 円錐切断面 | 円錐切断面は円錐の頂点を通る(下記の母線とは円錐の頂点から底面の円周上の点までを結ぶ線分のこと) | |||||
| 円錐の頂点のみと交わる平面 | 対の円錐の両方の母線と交わり頂点を通る平面 |
円錐の母線と平行で頂点を通る平面 (この場合は重なった1直線となる) |
||||
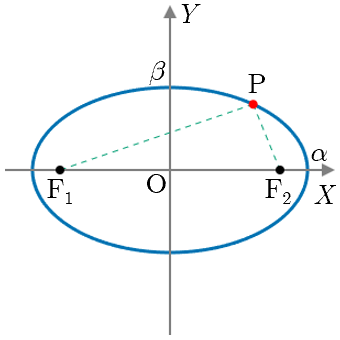
楕円(横長:焦点 , が 軸上に存在)
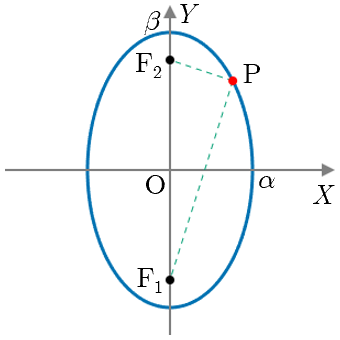
楕円(縦長:焦点 , が 軸上に存在)
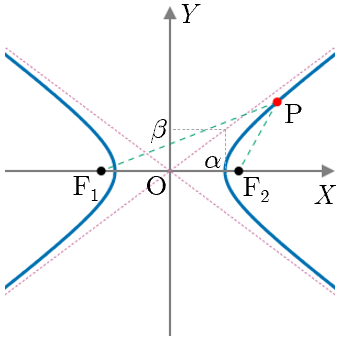
双曲線(横向き:焦点 , が 軸上に存在)
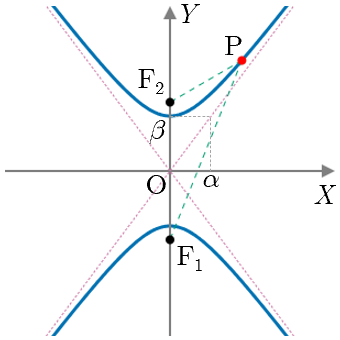
双曲線(縦向き:焦点 , が 軸上に存在)
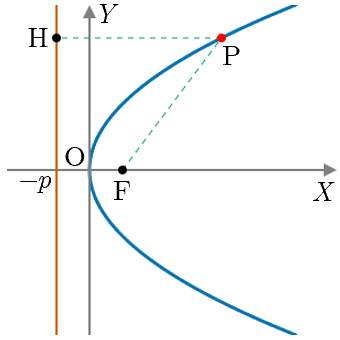
放物線(横向き:焦点 が 軸上に存在)
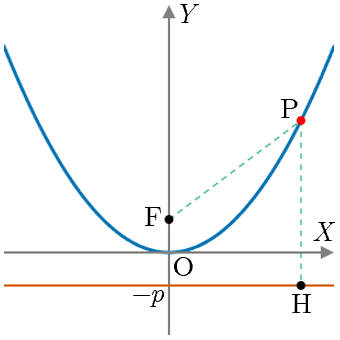
放物線(縦向き:焦点 が 軸上に存在)
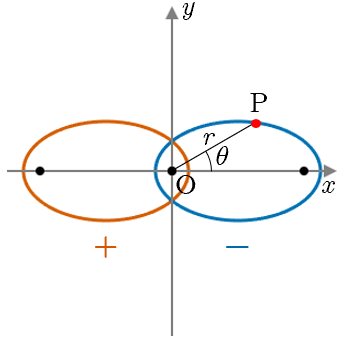
楕円(横長)
極方程式の分母2項目の符号が+なら右
の焦点,ーなら左の焦点が原点となる
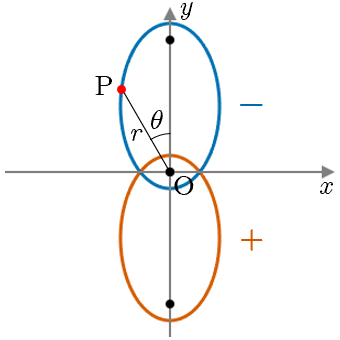
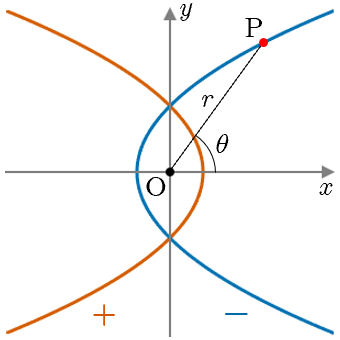
楕円(縦長)
極方程式の分母2項目の符号が+なら上
の焦点,ーなら下の焦点が原点となる
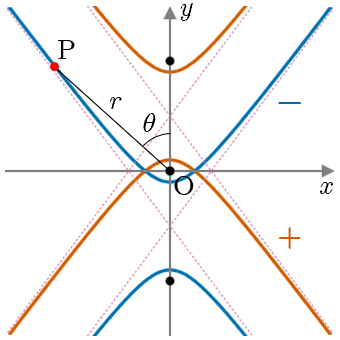
双曲線(横向き)
極方程式の分母2項目の符号が+なら左
の焦点,ーなら右の焦点が原点となる
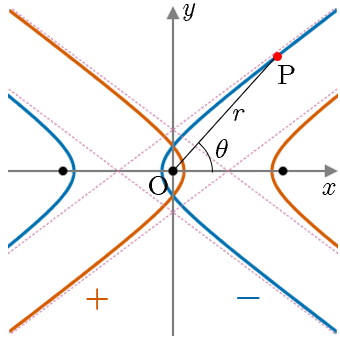
双曲線(縦向き)
極方程式の分母2項目の符号が+なら下
の焦点,ーなら上の焦点が原点となる
放物線(横向き)
極方程式の分母2項目の符号が
+なら右に凸,ーなら左に凸となる
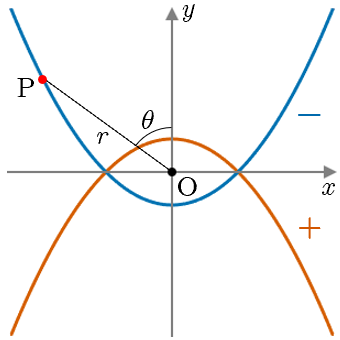
放物線(縦向き)
極方程式の分母2項目の符号が
+なら上に凸,ーなら下に凸となる
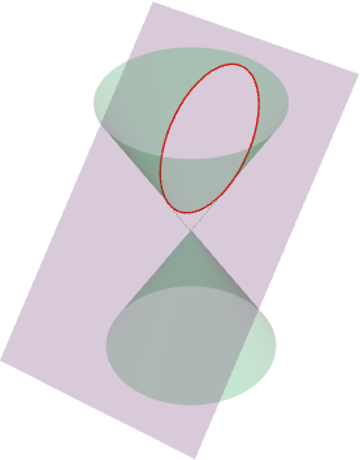
円錐曲線(楕円)
円錐切断面は対の円錐の片方の母線と交わる
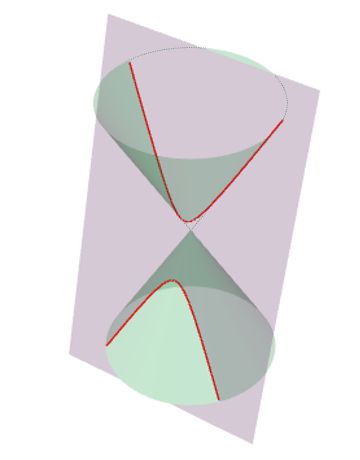
円錐曲線(双曲線)
円錐切断面は対の円錐の両方の母線と交わる
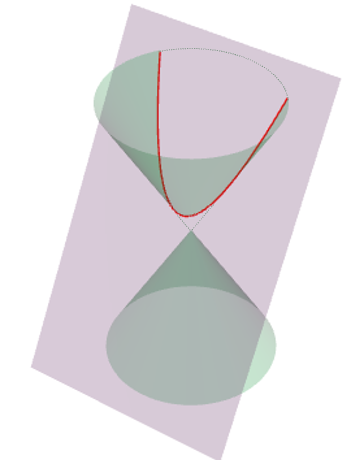
円錐曲線(放物線)
円錐切断面は円錐の母線と平行
ホーム>>カテゴリー分類>>幾何>>図と方程式>>2次曲線の分類
最終更新日:2025年10月7日