点から直線
への垂線の長さ(言い換えると 点
と直線 との距離)は
となる.
■導出計算
直線と点
の距離を求める.
直線
の方程式はで,
点の座標は
で ある.
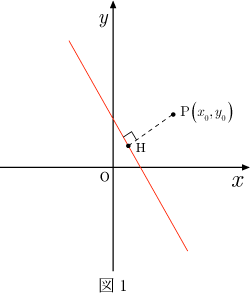
点から直線
に垂線を下ろし,直線との交点をとする. 線分の長さが直線と点の距離である.(図1)
計算を簡単にするために,点と直線を軸方向に,軸方向に
平行移動し,点
を原点に重ねる.
直線は,平行移動により
・・・・(1)
で表わされる直線に移る.
また,点は点に移る.(図2)
平行移動しただけであるので
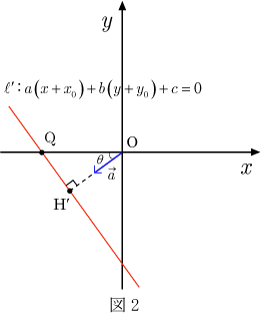
である.
直線と軸の交点をとする.
直線の傾きと等しく
より,である.
線分
より線分の傾きをとすると
(垂直に交わる条件を参照)
となり
となる.
よって,線分に平行なベクトルをとすると
である.
とのなす角をとすると
・・・・(2)
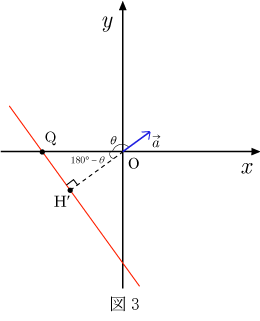
となる.がと逆向きの場合もある(図3).その場合
・・・・(3)
となる.よって(2),(3)より
となる.
点の座標を求める.(1)において,より
よって点の座標は
である.
より
ホーム>>カテゴリー別分類>>幾何>>垂線の長さ(点と直線)>>垂線の長さ(点と直線)その2
最終更新日:
2025年10月16日


