2直線が垂直に交わる条件

2つの直線の傾きを ${\displaystyle m_1}$ ， ${\displaystyle m_2}$  とすると，垂直に交わる(直交する)ための条件は

${\displaystyle m_1{m}_2=-1}$

である．

参考ページ：2直線のなす角

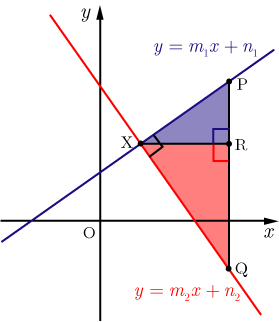
■証明

${\displaystyle m_1>0,m_2<0}$  とする．2つの直線の交点を ${\displaystyle \text{X}}$ ，交点 ${\displaystyle \text{X}}$ の右側に y  軸に平行な直線を引き，傾きが ${\displaystyle m_1}$ の直線との交点を ${\displaystyle \text{P}}$ ，傾きが ${\displaystyle m_2}$ の直線との交点を ${\displaystyle \text{Q}}$ とする．交点Xを通り， x  軸に平行な直線を引き，直線 ${\displaystyle \text{PQ}}$ との交点を ${\displaystyle \text{R}}$ とする．以上のように，点 ${\displaystyle \text{X}}$ ， ${\displaystyle \text{P}}$ ， ${\displaystyle \text{Q}}$ ， ${\displaystyle \text{R}}$ をとると△ ${\displaystyle \text{XRP}}$ ，△ ${\displaystyle \text{XRQ}}$ は直角三角形になる．

直線の傾きの定義より

${\displaystyle \frac{\text{PR}}{\text{XR}}=m_1}$  ･･････(1)

${\displaystyle \frac{\text{QR}}{\text{XR}}=-m_2}$  ･･････(2)

△${\displaystyle \text{XRP}}$が直角三角形より，三平方の定理が成り立つので

${\displaystyle {\text{XP}}^{\text{2}}={\text{XR}}^2+{\text{PR}}^2}$

${\displaystyle ={\text{XR}}^2+{\left(\text{XR}·m_1\right)}^2}$    (∵(1))

${\displaystyle ={\text{XR}}^2\left(1+{m_1}^2\right)}$  ･･････(3)

△ ${\displaystyle \text{XRQ}}$ が直角三角形より，三平方の定理が成り立つので

${\displaystyle {\text{XQ}}^{\text{2}}={\text{XR}}^2+{\text{QR}}^2}$

${\displaystyle ={\text{XR}}^2+{\left(-\text{XR}·m_2\right)}^2}$     (∵(2))

${\displaystyle ={\text{XR}}^2\left(1+{m_2}^2\right)}$  ･･････(4)

2つの直線が垂直に交わると， ${\displaystyle \angle \text{PXQ=90}°}$ となり△ ${\displaystyle \text{PXQ}}$ は直角三角形になる．よって，三平方の定理より

${\displaystyle {\text{PQ}}^{\text{2}}={\text{XP}}^2+{\text{XQ}}^2}$

${\displaystyle {\left(\text{PR}+\text{QR}\right)}^2}$ ${\displaystyle ={\text{XR}}^2\left(1+{m_1}^2\right)+{\text{XR}}^2\left(1+{m_2}^2\right)}$     (∵(3)，(4))

${\displaystyle {\left(\text{XR}·m_1-\text{XR}·m_2\right)}^2}$ ${\displaystyle ={\text{XR}}^2\left(1+{m_1}^2\right)+{\text{XR}}^2\left(1+{m_2}^2\right)}$     (∵(1)，(2))

${\displaystyle {\text{XR}}^2{\left(m_1-m_2\right)}^2}$ ${\displaystyle ={\text{XR}}^2\left(1+{m_1}^2\right)+{\text{XR}}^2\left(1+{m_2}^2\right)}$

${\displaystyle {\left(m_1-m_2\right)}^2}$ ${\displaystyle =\left(1+{m_1}^2\right)+\left(1+{m_2}^2\right)}$

${\displaystyle {m_1}^2-2m_1{m}_2+{m_2}^2}$ ${\displaystyle =2+{m_1}^2+{m_2}^2}$

${\displaystyle -2m_1{m}_2=2}$

$m_1{m}_2=-1$

2直線が垂直に交わると， ${\displaystyle m_1{m}_2=-1}$ である．

一方， ${\displaystyle m_1{m}_2=-1}$  ならば

${\displaystyle {\text{PQ}}^{\text{2}}-({\text{XP}}^2+{\text{XQ}}^2)}$

${\displaystyle ={\left(\text{PR}+\text{QR}\right)}^2-{\text{XP}}^2-{\text{XQ}}^2}$

${\displaystyle ={\left(\text{XR}·m_1-\text{XR}·m_2\right)}^2}$ ${\displaystyle -{\text{XR}}^2\left(1+m_1{}^2\right)}$ ${\displaystyle -{\text{XR}}^2\left(1+{m_2}^2\right)}$     (∵(1)，(2)，(3)，(4))

${\displaystyle ={\text{XR}}^2{\left(m_1-m_2\right)}^2-{\text{XR}}^2\left(1+{m_1}^2\right)}$ ${\displaystyle -{\text{XR}}^2\left(1+{m_2}^2\right)}$

${\displaystyle ={\text{XR}}^2\left(-2m_1{m}_2-2\right)}$

${\displaystyle ={\text{XR}}^2\left\{-2\left(-1\right)-2\right\}}$

${\displaystyle ={\text{XR}}^2\cdot 0}$

${\displaystyle =0}$

よって

${\displaystyle {\text{PQ}}^{\text{2}}={\text{XP}}^2+{\text{XQ}}^2}$

となり，△ ${\displaystyle \text{PXQ}}$ において三平方の定理がなりたち，△ ${\displaystyle \text{PXQ}}$ は直角三角形である．よって

${\displaystyle \angle \text{PXQ=90}°}$

すなわち，2直線は垂直に交わる．

以上より，証明された．

 

ホーム>>カテゴリー別分類>>幾何>>2直線が垂直に交わる条件

最終更新日 2026年9月6日