|
|||||||||||||
|
|||||||||||||
|
関連するページを見るにはこの知識グラフを利用してください.
問題リスト←このページに関連している問題です
アークサインとアークコサインの関係
, の間には
ただし, ・・・・・・(1)
の関係がある.
◆導出
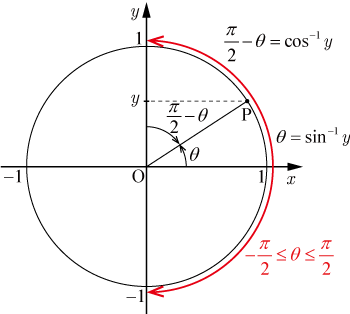
図のように単位円上に点 があり, 軸の正方向と線分 のなす角を とし, 軸の正方向と線分 のなす角を とすると
・・・・・・(2)
・・・・・・(3)
の関係がある. , の逆関数が存在するためには, の範囲は
・・・・・・(4)
(2)より
・・・・・・(5)
(3)より
・・・・・・(6)
が得られる.(6)に(5)を代入し、式を整理すると
となる.
【参考】
(2)と(3)より
が得られる.三角関数の計算の基礎を参照
●グラフを用いた説明
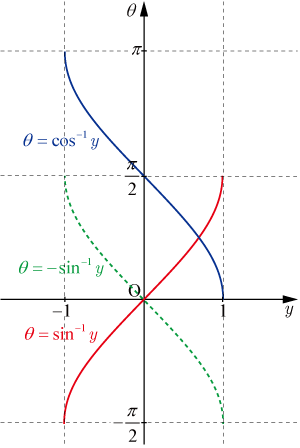
のグラフを 軸に関して対称移動した
のグラフをさらに 軸方向に 平行移動した
グラフは
のグラフのグラフと重なる.
よって
の関係が得られる.
ホーム>>カテゴリー分類>>三角関数>>アークサインとアークコサインの関係
最終更新日: 2024年8月2日