|
|||||||||||||
|
|||||||||||||
|
関連するページを見るにはこのグラフ図を利用してください.
逆関数
関数 がある.この関数においては,変数 に対してただ1つの値 が定まる.逆に を決めると がただ1つ定まる場合がある.この場合, は の関数となり
と表わすとする.
関数を表すとき,一般的に変数に,変数に対応する値に を用いるので
と書き直す.この関数を関数の逆関数という.逆写像参照のこと.
関数 の逆関数を一般的にと表す.
関数 において,とが1対1の対応になっている場合,関数 の逆関数が存在し
が成り立つ.
■事例
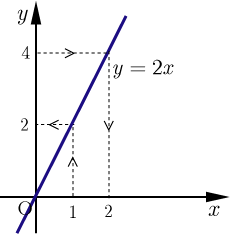 関数 (右の図の青線)について逆関数を考えてみる.
関数 (右の図の青線)について逆関数を考えてみる.
変数の値が1であれば, の値は2に定まる.逆に の値が4であれば, 値は2にただ1つ定まる.すなわち, を変数として を表すと
となる. とを入れ替えると
となり,これが,関数の逆関数(下の図の赤線)になる.
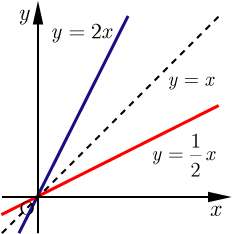
関数 のグラフとその関数の逆関数 のグラフは直線 に関して対称である.
関数 の場合は, の値4に対して は2と-2が対応し,1つに定まらない.よって, は 関数とならないが, と定義域の範囲を定めると, に対してただ1つの が定まり逆関数が存在することになる.
最終更新日 2023年12月5日