cos関数の合成(複素数を用いた導出) (composition of cosine functions (derivation using complex numbers))

２つのcos関数 $r_{1} \cos θ_{1}$ , $r_{2} \cos θ_{2}$ の合成式を，複素数を用いて表すと

$r_{1} \cos θ_{1} + r_{2} \cos θ_{2}$ $= Re [r_{1} e^{ⅈ θ_{1}} + r_{2} e^{ⅈ θ_{2}}]$ ---- (1)

$r_{1} e^{ⅈ θ_{1}} + r_{2} e^{ⅈ θ_{2}}$

$= \frac{r_{1} + r_{2}}{2} (e^{ⅈ θ_{1}} + e^{ⅈ θ_{2}}) + \frac{r_{1} - r_{2}}{2} (e^{ⅈ θ_{1}} - e^{ⅈ θ_{2}})$

$= \frac{r_{1} + r_{2}}{2} \exp [ⅈ \frac{θ_{1} + θ_{2}}{2}] (\exp [ⅈ \frac{θ_{1} - θ_{2}}{2}] + \exp [- ⅈ \frac{θ_{1} - θ_{2}}{2}])$

$+ \frac{r_{1} - r_{2}}{2} \exp [ⅈ \frac{θ_{1} + θ_{2}}{2}] (\exp [ⅈ \frac{θ_{1} - θ_{2}}{2}] - \exp [- ⅈ \frac{θ_{1} - θ_{2}}{2}])$

$= \exp [ⅈ \frac{θ_{1} + θ_{2}}{2}] {(r_{1} + r_{2}) \cos \frac{θ_{1} - θ_{2}}{2} + ⅈ (r_{1} - r_{2}) \sin \frac{θ_{1} - θ_{2}}{2}}$ ---- (2)

上式において

$a = (r_{1} + r_{2}) \cos \frac{θ_{1} - θ_{2}}{2}$ , $b = (r_{1} - r_{2}) \sin \frac{θ_{1} - θ_{2}}{2}$ , $θ = \frac{θ_{1} + θ_{2}}{2}$ ---- (3)

とおくと

$r_{1} e^{ⅈ θ_{1}} + r_{2} e^{ⅈ θ_{2}} = e^{ⅈ θ} (a + b ⅈ)$ $= e^{ⅈ θ} \cdot r e^{ⅈ φ}$ $= r e^{ⅈ (θ + φ)}$ ---- (4)

となる．ここで，

$r = \sqrt{a^{2} + b^{2}}$ $= \sqrt{r_{1}^{2} + r_{2}^{2} + 2 r_{1} r_{2} \cos (θ_{1} - θ_{2})}$ ---- (5)

$\tan φ = \frac{b}{a}$ $= \frac{r_{1} - r_{2}}{r_{1} + r_{2}} \tan \frac{θ_{1} - θ_{2}}{2}$ ---- (6)

である．したがって，

$r_{1} \cos θ_{1} + r_{2} \cos θ_{2}$ $= Re [r_{1} e^{ⅈ θ_{1}} + r_{2} e^{ⅈ θ_{2}}]$ $= Re [r e^{ⅈ (θ + φ)}]$ $= r \cos (θ + φ)$

を得る．（導出完了）

（※）式(1)の複素数を用いた表現において

$r_{1} \cos θ_{1} + r_{2} \cos θ_{2}$ $= Re [r_{1} e^{ⅈ θ_{1}} + r_{2} e^{- ⅈ θ_{2}}]$ ---- (7)

として同様に進めると，

$r_{1} e^{ⅈ θ_{1}} + r_{2} e^{- ⅈ θ_{2}} = r e^{ⅈ (θ + φ)}$ ---- (8)

$r = \sqrt{r_{1}^{2} + r_{2}^{2} + 2 r_{1} r_{2} \cos (θ_{1} + θ_{2})}$ , $θ = \frac{θ_{1} - θ_{2}}{2}$ , $\tan φ = \frac{r_{1} - r_{2}}{r_{1} + r_{2}} \tan \frac{θ_{1} + θ_{2}}{2}$ ---- (9)

が得られる．

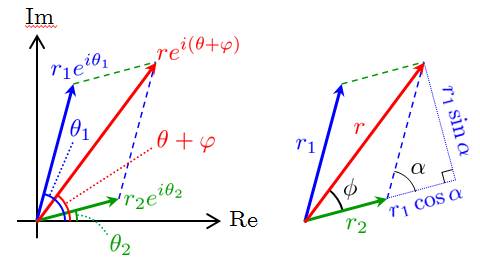
■ 複素平面での幾何学的な意味

図に示すように，複素数の和

$r_{1} e^{ⅈ θ_{1}} + r_{2} e^{ⅈ θ_{2}} = r e^{ⅈ (θ + φ)}$

は，複素平面上での2つのベクトルの和に対応する．右側の図中の角 $α$ は，

$α = θ_{1} - θ_{2}$ ---- (10)

であり，余弦定理により

$r = \sqrt{r_{1}^{2} + r_{2}^{2} - 2 r_{1} r_{2} \cos (π - α)}$
$= \sqrt{r_{1}^{2} + r_{2}^{2} + 2 r_{1} r_{2} \cos α}$ ---- (11)

である．また，角 $ϕ$ は次式を満たす．

$\tan ϕ = \frac{r_{1} \sin α}{r_{1} \cos α + r_{2}}$ ---- (12)

図から分かるように， $θ + φ = θ_{2} + ϕ$ であり， $θ = (θ_{1} + θ_{2}) / 2$ なので

$φ = θ_{2} + ϕ - \frac{θ_{1} + θ_{2}}{2}$ $= ϕ - \frac{θ_{1} - θ_{2}}{2}$ $= ϕ - \frac{α}{2}$ ---- (13)

となる．したがって，

$\tan φ = \tan (ϕ - \frac{α}{2})$ $= \frac{\tan ϕ - \tan \frac{α}{2}}{1 + \tan ϕ \tan \frac{α}{2}}$   （ $∵$ 加法定理）
       $= \frac{\frac{r_{1} \sin α}{r_{1} \cos α + r_{2}} - \tan \frac{α}{2}}{1 + \frac{r_{1} \sin α}{r_{1} \cos α + r_{2}} \tan \frac{α}{2}}$ $= \frac{r_{1} \sin α - (r_{1} \cos α + r_{2}) \tan \frac{α}{2}}{r_{1} \cos α + r_{2} + r_{1} \sin α \tan \frac{α}{2}}$
       $= \frac{2 r_{1} \sin \frac{α}{2} \cos \frac{α}{2} - r_{1} (2 \cos^{2} \frac{α}{2} - 1) \tan \frac{α}{2} - r_{2} \tan \frac{α}{2}}{r_{1} (1 - 2 \sin^{2} \frac{α}{2}) + r_{2} + 2 r_{1} \sin \frac{α}{2} \cos \frac{α}{2} \tan \frac{α}{2}}$   （ $∵$ 2倍角の公式）
       $= \frac{(r_{1} - r_{2}) \tan \frac{α}{2}}{r_{1} + r_{2}}$ $= \frac{r_{1} - r_{2}}{r_{1} + r_{2}} \tan \frac{θ_{1} - θ_{2}}{2}$     ---- (14)

が得られる．

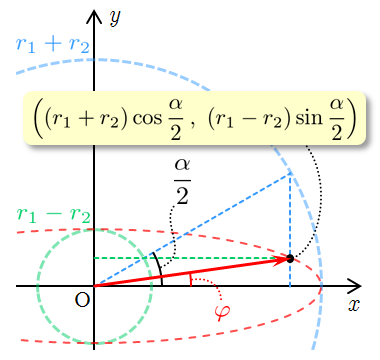
また，式(2)の表現

$r_{1} e^{ⅈ θ_{1}} + r_{2} e^{ⅈ θ_{2}}$ $= e^{ⅈ θ} {(r_{1} + r_{2}) \cos \frac{α}{2} + ⅈ (r_{1} - r_{2}) \sin \frac{α}{2}}$ ---- (15)

（ $θ = (θ_{1} + θ_{2}) / 2$ ， $α = θ_{1} - θ_{2}$ ）において，右辺の ${}$ 内は，長径を $r_{1} + r_{2}$ ，短径を $r_{1} - r_{2}$ とした複素平面上の楕円軌道を表している．その楕円軌道上の，角 $α / 2$ のときの位置ベクトルは $x y$ 平面上で

${\vec{r}}_{φ} = ((r_{1} + r_{2}) \cos \frac{α}{2}, (r_{1} - r_{2}) \sin \frac{α}{2})$

と表され，その大きさが

$r = | {\vec{r}}_{φ} |$
$= \sqrt{{(r_{1} + r_{2})}^{2} \cos^{2} \frac{α}{2} + {(r_{1} - r_{2})}^{2} \sin^{2} \frac{α}{2}}$
$= \sqrt{r_{1}^{2} + r_{2}^{2} + 2 r_{1} r_{2} \cos α}$

であり， $x$ 軸とのなす角 $φ$ が

$\tan φ = \frac{(r_{1} - r_{2}) \sin \frac{α}{2}}{(r_{1} + r_{2}) \cos \frac{α}{2}}$ $= \frac{r_{1} - r_{2}}{r_{1} + r_{2}} \tan \frac{α}{2}$

を満たす（ただし， $α = \pm π$ のとき $φ = \pm π / 2$ とする）．したがって，

${\vec{r}}_{φ} = (r \cos φ, r \sin φ)$

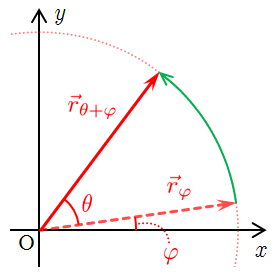
と表される．さらに，式(15)の右辺の指数関数 $e^{ⅈ θ}$ は，複素平面上のベクトルを原点の周りに角 $θ$ だけ回転させることに対応するので， ${\vec{r}}_{φ}$ を $θ$ 回転させると

${\vec{r}}_{φ} \to {\vec{r}}_{θ + φ}$ $= (r \cos (θ + φ), r \sin (θ + φ))$

となる．したがって，

${\vec{r}}_{θ + φ} \Leftrightarrow r e^{ⅈ (θ + φ)} = r_{1} e^{ⅈ θ_{1}} + r_{2} e^{ⅈ θ_{2}}$

という対応がある．

ホーム>>カテゴリー分類>>三角関数>>加法定理>>cos関数の合成（複素数を用いた導出）

最終更新日：2024年9月30日