${\displaystyle \left(\overrightarrow{a}+\overrightarrow{b}\right)\times \overrightarrow{c}}$${\displaystyle =\overrightarrow{a}\times \overrightarrow{c}+\overrightarrow{b}\times \overrightarrow{c}}$

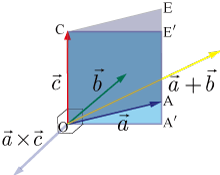
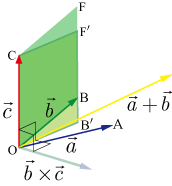
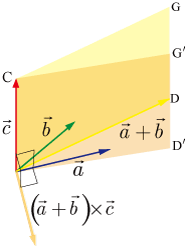
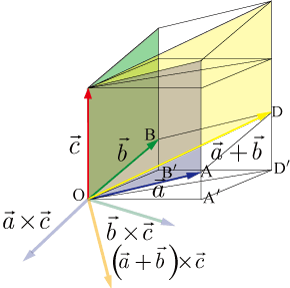
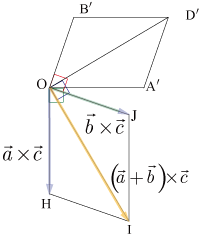
外積の分配法則が成り立つのを図を使い簡単に説明する．

点${\displaystyle \text{A}}$ を通り ${\displaystyle \overrightarrow{c}}$ に平行な直線に点${\displaystyle \text{O}}$ からおろした垂線の足を点${\displaystyle {\text{A}}^{\prime }}$ とすると，平行四辺形${\displaystyle \text{OAEC}}$ の面積＝長方形${\displaystyle \text{O}{\text{A}}^{\prime }{\text{E}}^{\prime }\text{C}}$の面積となる．よって

${\displaystyle {\text{OA}}^{\prime }=\frac{\left|\overrightarrow{a}\times \overrightarrow{c}\right|}{\left|\overrightarrow{c}\right|}}$

（平行四辺形${\displaystyle \text{OAEC}}$の面積＝ ${\displaystyle \left|\overrightarrow{a}\times \overrightarrow{c}\right|}$ ，長方形${\displaystyle \text{O}{\text{A}}^{\prime }{\text{E}}^{\prime }\text{C}}$の面積＝${\displaystyle \left|\overrightarrow{c}\right|{\text{OA}}^{\prime }}$より）

となる．同様にして

${\displaystyle {\text{OB}}^{\prime }=\frac{\left|\overrightarrow{b}\times \overrightarrow{c}\right|}{\left|\overrightarrow{c}\right|}}$ ，${\displaystyle {\text{OD}}^{\prime }=\frac{\left|\left(\overrightarrow{a}+\overrightarrow{b}\right)\times \overrightarrow{c}\right|}{\left|\overrightarrow{c}\right|}}$  

となる．

また，${\displaystyle \text{O}{\text{A}}^{\prime }}$，${\displaystyle \text{O}{\text{B}}^{\prime }}$，${\displaystyle \text{O}{\text{D}}^{\prime }}$は ${\displaystyle \overrightarrow{c}}$ に垂直で， ${\displaystyle \overrightarrow{a}\times \overrightarrow{c}}$ ，${\displaystyle \overrightarrow{b}\times \overrightarrow{c}}$，${\displaystyle \left(\overrightarrow{a}+\overrightarrow{b}\right)\times \overrightarrow{c}}$ も ${\displaystyle \overrightarrow{c}}$ に垂直である．よって，${\displaystyle \text{O}{\text{A}}^{\prime }}$，${\displaystyle \text{O}{\text{B}}^{\prime }}$，${\displaystyle \text{O}{\text{D}}^{\prime }}$， ${\displaystyle \overrightarrow{a}\times \overrightarrow{c}}$ ， ${\displaystyle \overrightarrow{b}\times \overrightarrow{c}}$ ， ${\displaystyle \left(\overrightarrow{a}+\overrightarrow{b}\right)\times \overrightarrow{c}}$ は同一平面上にある．

さらに，外積の定義より， ${\displaystyle \text{O}{\text{A}}^{\prime }}$と ${\displaystyle \overrightarrow{a}\times \overrightarrow{c}}$ ，${\displaystyle \text{O}{\text{B}}^{\prime }}$と ${\displaystyle \overrightarrow{b}\times \overrightarrow{c}}$ ，${\displaystyle \text{O}{\text{D}}^{\prime }}$と ${\displaystyle \left(\overrightarrow{a}+\overrightarrow{b}\right)\times \overrightarrow{c}}$ は垂直な関係である．

以上より，下図を参照すると，平行四辺形${\displaystyle \text{O}{\text{A}}^{\prime }{\text{D}}^{\prime }{\text{B}}^{\prime }}$を点${\displaystyle \text{O}}$ を中心として90°時計方向に回転し，${\displaystyle \left|\overrightarrow{c}\right|}$ 倍したものが平行四辺形${\displaystyle \text{OHIJ}}$ となる．

したがって，

${\displaystyle \left(\overrightarrow{a}+\overrightarrow{b}\right)\times \overrightarrow{c}=\overrightarrow{a}\times \overrightarrow{c}+\overrightarrow{b}\times \overrightarrow{c}}$ 

となる．

●${\displaystyle \overrightarrow{a}\times \left(\overrightarrow{b}+\overrightarrow{c}\right)=\overrightarrow{a}\times \overrightarrow{b}+\overrightarrow{a}\times \overrightarrow{c}}$ について

${\displaystyle \overrightarrow{a}\times \left(\overrightarrow{b}+\overrightarrow{c}\right)}$${\displaystyle =-\left(\overrightarrow{b}+\overrightarrow{c}\right)\times \overrightarrow{a}}$

${\displaystyle =-\left\{\left(\overrightarrow{b}+\overrightarrow{c}\right)\times \overrightarrow{a}\right\}}$

${\displaystyle =-\left(\overrightarrow{b}\times \overrightarrow{a}+\overrightarrow{c}\times \overrightarrow{a}\right)}$

${\displaystyle =-\overrightarrow{b}\times \overrightarrow{a}-\overrightarrow{c}\times \overrightarrow{a}}$

${\displaystyle =\overrightarrow{a}\times \overrightarrow{b}+\overrightarrow{a}\times \overrightarrow{c}}$

　

ホーム>>カテゴリー分類>>ベクトル>>外積>> ${\displaystyle \left(\overrightarrow{a}+\overrightarrow{b}\right)\times \overrightarrow{c}}$${\displaystyle =\overrightarrow{a}\times \overrightarrow{c}+\overrightarrow{b}\times \overrightarrow{c}}$

最終更新日 2023年2月20日