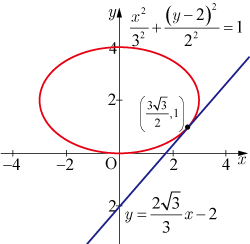問題を解くのに必要な知識を確認するにはこのグラフ図を利用してください．

陰関数の微分に関する問題

■問題

陰関数の微分法を用いて曲線 ${\displaystyle 4x^2+9y^2-36y=0}$ の ${\displaystyle \frac{dy}{dx}}$ を求め，曲線上の点 ${\displaystyle \left(\frac{3\sqrt{3}}{2},1\right)}$ における接線方程式を求めよ．

■解説動画

◇微分の動画一覧のページへ

■答

${\displaystyle \frac{dy}{dx}=6t^2\sqrt{t-1}}$

接線の方程式： ${\displaystyle y=24x+27}$

■解説

陰関数の微分法より

${\displaystyle 4x^2+9y^2-36y=0}$ ･･････(1)

の両辺を $x$ で微分する．

${\displaystyle \frac{d}{dx}\left(4x^2+9y^2-39y\right)=\frac{d}{dx}0}$

${\displaystyle \frac{d}{dx}4x^2+\frac{d}{dx}9y^2-\frac{d}{dx}36y=0}$

${\displaystyle 8x+18y\frac{dy}{dx}-36\frac{dy}{dx}=0}$

${\displaystyle 18\left(y-2\right)\frac{dy}{dx}=-8x}$

${\displaystyle \frac{dy}{dx}=-\frac{4x}{9\left(y-2\right)}}$ ･･････(2)

よって，点 ${\displaystyle \left(\frac{3\sqrt{3}}{2},1\right)}$ における接線の傾きは

${\displaystyle \frac{dy}{dx}=-\frac{4\cdot \frac{3\sqrt{3}}{2}}{9\left(1-2\right)}=\frac{2\sqrt{3}}{3}}$ ･･････(3)

となる．したがって，接線の方程式は

${\displaystyle y-1=\frac{2\sqrt{3}}{3}\left(x-\frac{3\sqrt{3}}{2}\right)}$

${\displaystyle y=\frac{2\sqrt{3}}{3}x-2}$ ･･････(4)

となる．

■備考

(1)を以下のように式変形をする．

${\displaystyle 4x^2+9\left(y^2-4y\right)=0}$

${\displaystyle 4x^2+9\left(y^2-4y+4-4\right)=0}$

${\displaystyle 4x^2+9\left(y^2-4y+4\right)=36}$

${\displaystyle 4x^2+9{\left(y-2\right)}^2=36}$

${\displaystyle \frac{x^2}{3^2}+\frac{{\left(y-2\right)}^2}{2^2}=1}$ ･･････(5)

(5)は楕円の方程式になる．(5)をさらに，以下のように式変形をする．

${\displaystyle \frac{{\left(y-2\right)}^2}{2^2}=1-\frac{x^2}{3^2}}$

${\displaystyle {\left(y-2\right)}^2=4\left(1-\frac{x^2}{3^2}\right)}$

${\displaystyle {\left(y-2\right)}^2=\frac{4}{9}\left(9-x^2\right)}$

${\displaystyle y-2=\pm \frac{2}{3}\sqrt{9-x^2}}$

${\displaystyle y=\pm \frac{2}{3}\sqrt{9-x^2}+2}$ ･･････(6)

${\displaystyle x=\frac{3\sqrt{3}}{2}}$ を(6)に代入する．

${\displaystyle y=\pm \frac{2}{3}\sqrt{9-{\left(\frac{3\sqrt{3}}{2}\right)}^2}+2}$ ${\displaystyle =\pm \frac{2}{3}\sqrt{9-\frac{27}{4}}+2}$ ${\displaystyle =\pm \frac{2}{3}\sqrt{\frac{9}{4}}+2}$ ${\displaystyle =\pm 1+2}$ ${\displaystyle =3,1}$ ･･････(7)

(7)より，点 ${\displaystyle \left(\frac{3\sqrt{3}}{2},1\right)}$ は，関数

${\displaystyle y=-\frac{2}{3}\sqrt{9-x^2}+2}$ ･･････(8)

のグラフ上の点である．(8)を $x$ で微分する．

${\displaystyle \frac{dy}{dx}=-\frac{2}{3}\cdot \frac{1}{2}\cdot \frac{1}{\sqrt{9-x^2}}\cdot \left(-2x\right)}$ ${\displaystyle =-\frac{-2x}{3\sqrt{9-x^2}}}$ ･･････(9)

よって，点 ${\displaystyle \left(\frac{3\sqrt{3}}{2},1\right)}$ における接線の傾きは，(9)より

${\displaystyle \frac{dy}{dx}=\frac{2\cdot \frac{3\sqrt{3}}{2}}{3\sqrt{9-{\left(\frac{3\sqrt{3}}{2}\right)}^2}}}$ ${\displaystyle =\frac{3\sqrt{3}}{3\sqrt{9-\frac{27}{4}}}}$ ${\displaystyle =\frac{\sqrt{3}}{\sqrt{\frac{9}{4}}}}$ ${\displaystyle =\frac{2\sqrt{3}}{3}}$

となる．

　

ホーム>>カテゴリー分類>>微分>>微分に関する演習問題>>微分の計算問題>>陰関数の微分に関する問題

最終更新日： 2025年4月30日

[ページトップ]

利用規約

google translate (English version)