双曲線の問題

■問題

双曲線 $\frac{{(x + 1)}^{2}}{4} - \frac{{(y - 2)}^{2}}{4} = - 1$ のグラフを描け(漸近線も入れよ)．さらに，頂点座標を求めよ．

■答

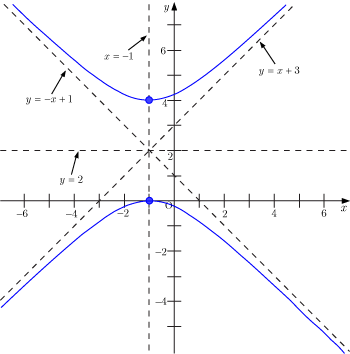
漸近線： ${\begin{matrix} y = x + 3 \\ y = - x + 1 \end{matrix}$

頂点座標： $(- 1, 4)$ ， $(- 1, 0)$

■解き方

$\frac{{(x + 1)}^{2}}{2^{2}} - \frac{{(y - 2)}^{2}}{2^{2}} = - 1$ ･･････(1)

このグラフは

$\frac{x^{2}}{2^{2}} - \frac{x^{2}}{2^{2}} = - 1$ ･･････(2)

のグラフを

$x$ 軸方向に $- 1$ ， $y$ 軸方向に $2$

平行移動したものである．

(2)のグラフの漸近線を $y = a x + b$ とすると

$\frac{x^{2}}{2^{2}} - \frac{y^{2}}{2^{2}} = - 1$ ， $\frac{y^{2}}{2^{2}} = \frac{x^{2}}{2^{2}} 1$ ， $y^{2} = x^{2} + 4$ ， $y = \pm \sqrt{x^{2} + 4}$ ， $f (x) = \pm \sqrt{x^{2} + 4}$

$a = \lim_{x \to \infty} \frac{f (x)}{x}$ $= \lim_{x \to \infty} \frac{\pm \sqrt{x^{2} + 4}}{\sqrt{x^{2}}}$ $= \lim_{x \to \infty} \pm \sqrt{1 + \frac{4}{x^{2}}}$ $= \pm 1$

$b = \lim_{x \to \pm \infty} \{f (x) - a x\}$ $= \lim_{x \to \pm \infty} \{\pm \sqrt{x^{2} + 4} - (\pm 1) x\}$ $= \lim_{x \to \pm \infty} \pm (\sqrt{x^{2} + 4} - x)$ $= \lim_{x \to \pm \infty} \pm \frac{(\sqrt{x^{2} + 4} - x) (\sqrt{x^{2} + 4} + x)}{(\sqrt{x^{2} + 4} + x)}$ $\lim_{x \to \pm \infty} \pm \frac{(x^{2} + 4) - x^{2}}{(\sqrt{x^{2} + 4} + x)}$ $= \lim_{x \to \pm \infty} \pm \frac{4}{(\sqrt{x^{2} + 4} + x)}$ $= 0$

よって，漸近線は

$y = \pm x$

で，頂点座標は

$(0, 2)$ ， $(0, - 2)$

である．

よって，(1)のグラフの頂点座標は

$(- 1, 4)$ ， $(- 1, 0)$

漸近線は

$y - 2 = x + 1 \to y = x + 3$

$y - 2 = - (x + 1) \to y = - x + 1$

よってグラフは下図のようになる．

ホーム>>カテゴリー分類>>関数>>関数の演習問題>>いろいろな方程式に関する問題>>双曲線の問題

最終更新日： 2024年9月13日