偶関数か奇関数かを判断する問題
■問題
次の関数は,偶関数,奇関数,どちらでもない,かを判定せよ.
(1)
(2)
(3)
■解説動画
■答
(1)
:奇関数
(2)
:偶関数でも奇関数でもない
(3)
:偶関数
■解説
(1)
について
となっていることより,
は奇関数である.
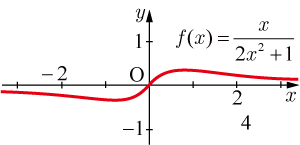
のグラフが 原点対称になっていることからも,奇関数であることが分かる.
(2)
について
,
となっていることより,
は偶関数でも奇関数でもない.
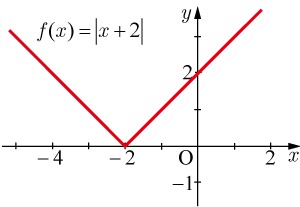
のグラフは,
に関して対称でもなければ,原点対称でもないことからも偶関数でも奇関数でもないことが分かる.
(3)
について
となっていることより,
は偶関数である.
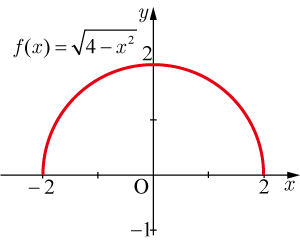
のグラフは,
に関して対称になっていることからも偶関数であることが分かる.
ホーム>>カテゴリー分類>>関数>>関数の演習問題>>1次関数,2次関数などに関する問題>>偶関数か奇関数かを判断する問題
最終更新日:
2025年4月27日


