拡大⇒平行移動に関する問題

■問題

関数 $y = \frac{2 x + 1}{x - 1}$ $y = \frac{2 x + 1}{x - 1}$ のグラフは， $y = \frac{1}{x}$ $y = \frac{1}{x}$ のグラフをどのように変形・移動したものか答え，グラフを描け．

■動画解説

◆関連動画のページへ

■答

主なものとして，以下の2つを例としてあげる．

$y = \frac{2 x + 1}{x - 1}$ $y = \frac{2 x + 1}{x - 1}$ のグラフは， $y = \frac{1}{x}$ $y = \frac{1}{x}$ のグラフを原点を中心に $x$ $x$ 軸方向に $3$ $3$ 倍に拡大した後， $x$ $x$ 軸方向に $1$ $1$ ， $y$ $y$ 軸方向に $2$ $2$ 平行移動したもの
$y = \frac{2 x + 1}{x - 1}$ $y = \frac{2 x + 1}{x - 1}$ のグラフは， $y = \frac{1}{x}$ $y = \frac{1}{x}$ のグラフを原点を中心に $y$ $y$ 軸方向に $3$ $3$ 倍に拡大した後， $x$ $x$ 軸方向に $1$ $1$ ， $y$ $y$ 軸方向に $2$ $2$ 平行移動したもの

■ヒント

関数 $y = f (x)$ $y = f (x)$ のグラフを原点を中心に $x$ $x$ 軸方向に $c$ $c$ 倍， $y$ $y$ 軸方向に $d$ $d$ 倍に拡大した後， $x$ $x$ 軸方向に $a$ $a$ ， $y$ $y$ 軸方向に $b$ $b$ 平行移動した（拡大→平行移動）グラフを表す関数

$\frac{y - b}{d} = f (\frac{x - a}{c})$ $\frac{y - b}{d} = f (\frac{x - a}{c})$ ･･････(1)

を参考にするとよい．

■解説

関数 $y = \frac{2 x + 1}{x - 1}$ $y = \frac{2 x + 1}{x - 1}$ を以下のように変形する

$y = \frac{2 x + 1}{x - 1}$ $y = \frac{2 x + 1}{x - 1}$ $= \frac{2 (x - 1) + 2 + 1}{x - 1}$ $= \frac{2 (x - 1) + 2 + 1}{x - 1}$ $= 2 + \frac{3}{x - 1}$ $= 2 + \frac{3}{x - 1}$

よって

$y - 2 = \frac{3}{x - 1}$ $y - 2 = \frac{3}{x - 1}$

となる．これを，更に(1)との対応関係が分かるように変形する．主なもとのとして以下の2つの式が考えられる．

$\frac{y - 2}{1} = \frac{1}{\frac{x - 1}{3}}$ $\frac{y - 2}{1} = \frac{1}{\frac{x - 1}{3}}$ ･･････(2)

(2)の両辺に $\frac{1}{3}$ $\frac{1}{3}$ を掛けると

$\frac{y - 2}{3} = \frac{1}{\frac{x - 1}{1}}$ $\frac{y - 2}{3} = \frac{1}{\frac{x - 1}{1}}$ ･･････(3)

となる．(1)と(2)を比較すると

$f (x) = \frac{1}{x}$ $f (x) = \frac{1}{x}$

$a = 1$ $a = 1$ ， $b = 2$ $b = 2$ ， $c = 3$ $c = 3$ ， $d = 1$ $d = 1$

になる．したがって，(2)より

$y = \frac{2 x + 1}{x - 1}$ $y = \frac{2 x + 1}{x - 1}$ のグラフは， $y = \frac{1}{x}$ $y = \frac{1}{x}$ のグラフを原点を中心に $x$ $x$ 軸方向に $3$ $3$ 倍に拡大した後， $x$ $x$ 軸方向に $1$ $1$ ， $y$ $y$ 軸方向に $2$ $2$ 平行移動したもの

になる．

(1)と(3)を比較すると

$f (x) = \frac{1}{x}$ $f (x) = \frac{1}{x}$

$a = 1$ $a = 1$ ， $b = 2$ $b = 2$ ， $c = 1$ $c = 1$ ， $d = 3$ $d = 3$

になる．したがって，(3)より

$y = \frac{2 x + 1}{x - 1}$ $y = \frac{2 x + 1}{x - 1}$ のグラフは， $y = \frac{1}{x}$ $y = \frac{1}{x}$ のグラフを原点を中心に $y$ $y$ 軸方向に $3$ $3$ 倍に拡大した後， $x$ $x$ 軸方向に $1$ $1$ ， $y$ $y$ 軸方向に $2$ $2$ 平行移動したもの

になる．

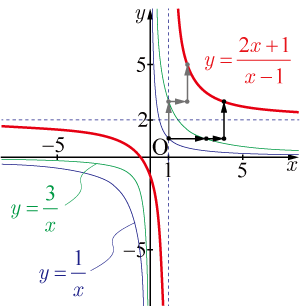
$y = \frac{2 x + 1}{x - 1}$ $y = \frac{2 x + 1}{x - 1}$ のグラフは答のところの図のようになる．

$y = \frac{1}{x}$ $y = \frac{1}{x}$ のグラフを原点を中心に $x$ $x$ 軸方向に3倍に拡大したグラフを表す関数は

$y = \frac{1}{\frac{x}{3}}$ $y = \frac{1}{\frac{x}{3}}$ ⇒　 $y = \frac{3}{x}$ $y = \frac{3}{x}$

$y = \frac{1}{x}$ $y = \frac{1}{x}$ のグラフを原点を中心に $y$ $y$ 軸方向に3倍に拡大したグラフを表す関数は

$\frac{y}{3} = \frac{1}{x}$ $\frac{y}{3} = \frac{1}{x}$ ⇒　 $y = \frac{3}{x}$ $y = \frac{3}{x}$

となり，どちらも同じグラフになる．このグラフを $x$ $x$ 軸方向に $1$ $1$ ， $y$ $y$ 軸方向に $2$ $2$ 平行移動したグラフを表す関数が，問題で提示された

$y - 2 = \frac{3}{x - 1}$ $y - 2 = \frac{3}{x - 1}$ ⇒　 $y = \frac{2 x + 1}{x - 1}$ $y = \frac{2 x + 1}{x - 1}$

となる．

■備考

今回の場合，(2)の両辺に掛ける値により原点を中心に $x$ $x$ 軸方向と $y$ $y$ 方向の倍率を任意に変化させることができる．

平行移動した後，拡大することも可能である．

ホーム>>カテゴリー分類>>関数>>関数の演習問題>>グラフの移動に関する問題>>拡大⇒平行移動に関する問題

最終更新日： 2025年2月9日

拡大⇒平行移動に関する問題

■問題

■動画解説

◆関連動画のページへ

■答

■ヒント

■解説

■備考

Chat window