|
|||||||||||||
|
|||||||||||||
|
問題を解くのに必要な知識を確認するにはこの知識グラフを利用してください.
絶対値の記号を含む関数のグラフの問題
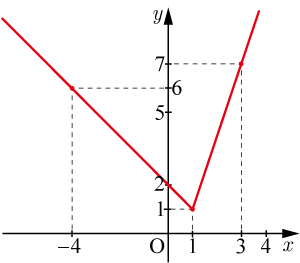
■問題
のフラフをかけ.
■解説動画
◆関連動画のページへ
■答
場合分けをして
・・・・・・(1)
を絶対値の記号を含まない式で表現をする.このとき,絶対値の性質1を用いる.
● ,すなわち, の場合
より,(1)は
・・・・・・(2)
となる.
● ,すなわち, の場合
より,(1)は
・・・・・・(3)
となる.
(1)を絶対値の記号を使わずに表現すると
となる.
グラフをかくと以下のようになる.グラフのかき方はこの問題やこの問題を参考にする.
ホーム>>カテゴリー分類>>関数>>関数の演習問題>>1次関数,2次関数などに関する問題>>絶対値の記号を含む関数のグラフの問題
最終更新日: 2025年4月27日