2次関数の　頂点　グラフ　最小値　切片

■問題

2次関数 ${\displaystyle y=3x^2-12x+9}$  について以下の問いに答えよ．

1. 頂点の座標を求めよ．
2. グラフを描け．
3. 最小値を求めよ．
4. $x$  切片， $y$  切片を求めよ．

■動画解説

◆関連動画のページへ

■答

1. 頂点の座標は ${\displaystyle \left(2,-3\right)}$
2. 最小値は， ${\displaystyle x=2}$  のときで， $-3$
3. グラフは解説をみよ．
4. $x$  切片 は $1$ ， $3$ ， $y$  切片 は $9$

■解説

2次関数 ${\displaystyle y=3x^2-12x+9}$  をグラフの特徴がわかるように以下のように式を変形（平方完成）する．

${\displaystyle x^2}$ の係数 $3$ で ${\displaystyle x^2}$ の項と ${\displaystyle x}$ の項をくくる．

${\displaystyle y=3\left(x^2-4x\right)+9}$

（ ）の中で $4$ をたして $4$ を引く．差し引き $0$ で値は変わらない．　

${\displaystyle =3\left(x^2-4x+4-4\right)+9}$

${\displaystyle =3\left\{{\left(x-2\right)}^2-4\right\}+9}$

${\displaystyle =3{\left(x-2\right)}^2+3\left(-4\right)+9}$

${\displaystyle =3{\left(x-2\right)}^2-3}$

よって，頂点の座標は ${\displaystyle \left(2,-3\right)}$  となる．

グラフを描くために更に式を変形する．

${\displaystyle y+3=3{\left(x-2\right)}^2}$  

${\displaystyle \frac{y+3}{3}={\left(\frac{x-2}{1}\right)}^2}$  

この式より，求めるグラフは，2次関数の最も単純な ${\displaystyle y=x^2}$ のグラフを，原点を中心として $y$ 軸方向 $3$ 倍（拡大）した後， $x$ 軸方向に $2$ ， $y$ 軸方向に $-3$ 平行移動したものである（拡大→平行移動を参照）．グラフを下の図に示す．

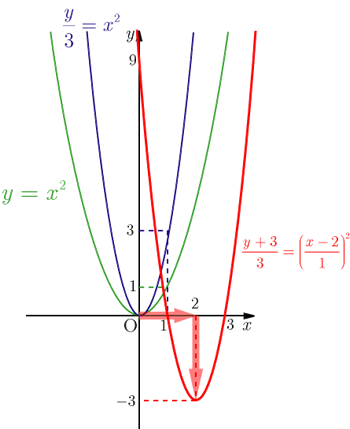最小値は， ${\displaystyle x=2}$ のときで， $-3$ となる．

$x$ 切片を求める．

${\displaystyle y=0}$ のときの $x$ の値であるので

$3x^2-12x+9=0$

の2次方程式を解けばよい．

因数分解する．

各項の共通因数である $3$ でくくる．

${\displaystyle 3\left(x^2-4x+3\right)=0}$

(　)の中をたすきがけで因数分解する．

${\displaystyle \begin{array}{lllll}1\hfill & {}_{\searrow }{}_{\nearrow }\hfill & -1\hfill & \to \hfill & -1\hfill \\ 1\hfill & {}^{\nearrow }{}^{\searrow }\hfill & -3\hfill & \to \hfill & -3\hfill \\ \hfill & \hfill & \hfill & \hfill & -4\hfill \end{array}}$

${\displaystyle 3\left(x-3\right)\left(x-1\right)=0}$

よって， ${\displaystyle x=1,3}$ となる．すなわち， $x$  切片 は $1$ ， $3$ となる．

$y$ 切片を求める．

${\displaystyle x=0}$  のときの $y$ の値であるので

${\displaystyle y=3\cdot 0^2-12\cdot 0+9}$

よって， ${\displaystyle y=9}$ となる．すなわち， $y$ 切片は $9$ となる．

 

ホーム>>カテゴリー分類>>関数>>関数の演習問題>>1次関数，2次関数などに関する問題>>2次関数の　頂点　グラフ　最小値　切片

最終更新日： 2025年2月20日