問題を解くのに必要な知識を確認するにはこのグラフ図を利用してください．

加法定理の問題

■問題

${\displaystyle cos\alpha =\frac{3}{5}}$ ， ${\displaystyle sin\beta =\frac{5}{13}}$ のとき， ${\displaystyle cos\left(\alpha +\beta \right)}$ ， ${\displaystyle tan\left(\alpha +\beta \right)}$ の値を求めよ．ただし， ${\displaystyle 0<\alpha \text{,}\beta <\frac{\pi }{2}}$ とする．

■解説動画

◇三角関数の動画一覧のページへ

■答

${\displaystyle cos\left(\alpha +\beta \right)=\frac{16}{65}}$ ， ${\displaystyle tan\left(\alpha +\beta \right)=\frac{63}{16}}$

■ヒント

${\displaystyle \cos \alpha }$ の値よりに ${\displaystyle \sin \alpha }$ の値を， ${\displaystyle \sin \beta }$ の値より ${\displaystyle \cos \beta }$ の値を算出する．また，加法定理を利用する．

■解き方

${\displaystyle 0<\alpha \text{,}\beta <\frac{\pi }{2}}$ のとき， ${\displaystyle sin\alpha >0}$ ， ${\displaystyle cos\beta >0}$ であるから

${\displaystyle cos\alpha =\frac{3}{5}}$ より

${\displaystyle sin\alpha =\sqrt{1-{cos}^2\alpha }}$ ${\displaystyle =\sqrt{1-{\left(\frac{3}{5}\right)}^2}}$ ${\displaystyle =\frac{4}{5}}$ ･･････(1) 　， ${\displaystyle tan\alpha =\frac{sin\alpha }{cos\alpha }=\frac{4}{3}}$ ･･････(2)

${\displaystyle sin\beta =\frac{5}{13}}$ より

${\displaystyle cos\beta =\sqrt{1-{cos}^2\alpha }}$ ${\displaystyle =\sqrt{1-{\left(\frac{5}{13}\right)}^2}}$ ${\displaystyle =\frac{12}{13}}$ ･･････(3)　， ${\displaystyle tan\beta =\frac{sin\beta }{cos\beta }=\frac{5}{12}}$ ･･････(4)

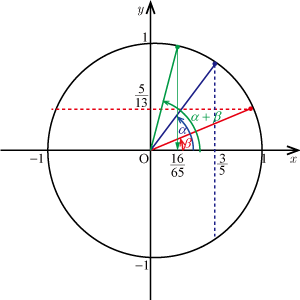
余弦（コサイン） の加法定理を利用し，(1)と(3)を代入すると

${\displaystyle cos\left(\alpha +\beta \right)}$ ${\displaystyle =cos\alpha cos\beta -sin\alpha sin\beta }$

${\displaystyle =\frac{3}{5}\times \frac{12}{13}-\frac{4}{5}\times \frac{5}{13}}$

${\displaystyle =\frac{36}{65}-\frac{20}{65}}$

${\displaystyle =\frac{16}{65}}$

正接（タンジェント） の加法定理を利用し，(2)と(4)を代入すると

${\displaystyle \tan \left(\alpha +\beta \right)}$

${\displaystyle =\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }}$

${\displaystyle =\frac{{\displaystyle \frac{4}{3}}+{\displaystyle \frac{5}{12}}}{1-{\displaystyle \frac{4}{3}}\times {\displaystyle \frac{5}{12}}}}$

${\displaystyle =\frac{{\displaystyle \frac{21}{12}}}{{\displaystyle \frac{4}{9}}}}$

${\displaystyle =\frac{63}{16}}$

 

ホーム>>カテゴリー分類>>三角関数>>三角関数の問題>>加法定理に関する問題>>加法定理の問題

学生スタッフ作成

最終更新日： 2025年5月30日

[ページトップ]

利用規約

google translate (English version)