積分を用いて面積を求める問題

■問題

曲線 $y = - x^{4} + 2 x^{3}$ ，直線 $x = 1$ ， $x$ 軸で囲まれた面積を求めよ．ただし， $x ≧ 1$ とする．

$\frac{13}{10}$

曲線と $x$ 軸で囲まれた面積の求め方

1．曲線のグラフを書く．

2．グラフと $x$ 軸との共有点と上下関係を調べて面積を求める．

$y = - x^{4} + 2 x^{3}$

$= - x^{3} (x - 2)$

$y = 0$ とすると， $x = 0, 2$

$y^{'} = - 4 x^{3} + 6 x^{2}$

$= - 2 x^{2} (2 x - 3)$

$y^{'} = 0$ とすると， $x = 0, \frac{3}{2}$

$y$ における増減表を次のようになる．

よって， $y = - x^{4} + 2 x^{3}$ ， $x$ 軸， $x = 1$ に囲まれた面積は図のようになる．

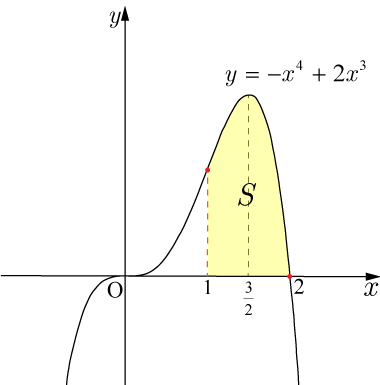
図より， $1 ≦ x ≦ 2$ のとき $y ≧ 0$ であるから，求める面積 $S$ は面積の計算より

$S = \int_{1}^{2} (- x^{4} + 2 x^{3}) d x$

$= {[- \frac{x^{5}}{5} + \frac{x^{4}}{2}]}_{1}^{2}$

$= (- \frac{2^{5}}{5} + \frac{2^{4}}{2}) - (- \frac{1^{5}}{5} + \frac{1^{4}}{2})$

$= \frac{13}{10}$

ホーム>>カテゴリー分類>>積分>>積分の問題>>定積分の問題>> $y = - x^{4} + 2 x^{3}$ ， $x$ 軸， $x = 1$ で囲まれる面積

学生スタッフ作成
最終更新日：2025年3月8日