弾性力のした仕事

■問題

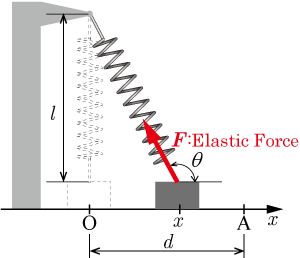
質量${\displaystyle M}$の物体があり，図のようにばねでつながれている．物体を原点から点${\displaystyle \text{A}}$までゆっくりと動かしたとき，弾性力(Elastic Force)のした仕事を求めよ．ただし，ばね定数は${\displaystyle k}$，ばねの自然長は${\displaystyle l}$とし，物体はばねの弾性力により持ち上がることはないとする．

■答

${\displaystyle -\frac{1}{2}k{\left(\sqrt{l^2+d^2}-l\right)}^2}$

■ヒント

弾性力，仕事

■解説

図のように物体の移動方向を${\displaystyle x}$軸の正方向とする．また，物体の位置を${\displaystyle x}$で表すこととする．

物体の位置が${\displaystyle x}$のときのばねの伸び${\displaystyle \Delta l}$は，${\displaystyle x}$まで移動したときのばねの長さから元のばねの長さ${\displaystyle l}$を引いたものである．

ここで，${\displaystyle x}$まで移動したときのばねの長さを${\displaystyle l^{\prime }}$とすると，${\displaystyle l^{\prime }}$は三平方の定理より

${\displaystyle l^{\prime }=\sqrt{l^2+x^2}}$ 　

したがって

${\displaystyle \Delta l=l^{\prime }-l}$${\displaystyle =\sqrt{l^2+x^2}-l}$ 　

よって，ばねの弾性力の大きさは

${\displaystyle =k\left(\sqrt{l^2+x^2}-l\right)}$ 　

となる．

図のように${\displaystyle x}$軸と弾性力のなす角を${\displaystyle \theta }$ とすると，三角関数の定義より

${\displaystyle \cos \theta =\frac{-x}{\sqrt{l^2+x^2}}}$${\displaystyle =-\frac{x}{\sqrt{l^2+x^2}}}$ 　

となる．

物体を位置${\displaystyle x}$から${\displaystyle dx}$だけ動かした時にかかる弾性力のした仕事　${\displaystyle dW}$は

${\displaystyle =k\left(\sqrt{l^2-x^2}-l\right)\cdot \left(-\frac{x}{\sqrt{l^2+x^2}}\right)dx}$${\displaystyle =-\frac{kx\left(\sqrt{l^2-x^2}-l\right)}{\sqrt{l^2+x^2}}dx}$

となる．従って，物体を原点${\displaystyle O}$から点${\displaystyle A}$まで動かした時の弾性力のした仕事　${\displaystyle W}$は

${\displaystyle W=-{\int }_0^d\frac{kx\left(\sqrt{l^2+x^2}-l\right)}{\sqrt{l^2+x^2}}dx}$ 　

${\displaystyle =-{\int }_0^d\left(kx-\frac{klx}{\sqrt{l^2+x^2}}\right)dx}$ 　

${\displaystyle =-{\int }_0^{d}kxdx+{\int }_0^d\frac{klx}{\sqrt{l^2+x^2}}dx}$ 　

${\displaystyle =-{\left[\frac{1}{2}k{x}^2\right]}_0^d+{\left[klt\right]}_l^{\sqrt{l^2+d^2}}}$ 　

(${\displaystyle {{\displaystyle \int }}_0^d\frac{klx}{\sqrt{l^2+x^2}}dx={\left[klt\right]}_l^{\sqrt{l^2+d^2}}}$ の計算はここを参照)

${\displaystyle =-\frac{1}{2}k{d}^2+kl\sqrt{l^2+d^2}+k{l}^2}$ 　

${\displaystyle =-\frac{1}{2}k\left(d^2-2l\sqrt{l^2+d^2}+2l^2\right)}$ 　

${\displaystyle =-\frac{1}{2}k\left(l^2+d^2-2l\sqrt{l^2+d^2}+l^2\right)}$ 　

${\displaystyle =-\frac{1}{2}k{\left(\sqrt{l^2+d^2}-l\right)}^2}$ 　

よって，物体を原点から点Aまでゆっくりと動かしたときの弾性力のした仕事は${\displaystyle -\frac{1}{2}k{\left(\sqrt{l^2+d^2}-l\right)}^2}$である．

　

ホーム>>カテゴリー分類>>積分>>積分の問題>>定積分の問題>>弾性力のした仕事

学生スタッフ作成
最終更新日： 2023年11月23日