問題を解くのに必要な知識を確認するにはこのグラフ図を利用してください．

因数分解

■問題

次の式を因数分解しなさい．

${\displaystyle x^2-x-72}$

■答

${\displaystyle \left(x+8\right)\left(x-9\right)}$

■ヒント

たすきがけ手法を利用する．

■解き方

因数分解の基本公式より

${\displaystyle ac{x}^2+\left(ad+bc\right)x+bd=x^2-x-72}$

すなわち

${\displaystyle ac=1}$ ，${\displaystyle ad+bc=-1}$ ，${\displaystyle bd=-72}$

であり，これを満たす${\displaystyle a}$ ，${\displaystyle b}$，${\displaystyle c}$，${\displaystyle d}$を求める．

${\displaystyle ac=1}$ を満たす整数${\displaystyle a}$，${\displaystyle c}$は

${\displaystyle \{\begin{array}{c}a=1\\ c=1\end{array}}$   ${\displaystyle \{\begin{array}{c}a=-1\\ c=-1\end{array}}$

${\displaystyle bd=-72}$ を満たす整数${\displaystyle b}$，${\displaystyle d}$は

${\displaystyle \{\begin{array}{c}b=-8\\ d=9\end{array}}$   ${\displaystyle \{\begin{array}{c}b=8\\ d=-9\end{array}}$   ${\displaystyle \{\begin{array}{c}b=6\\ d=-12\end{array}}$   ${\displaystyle \{\begin{array}{c}b=-6\\ d=12\end{array}}$

これをたすきがけ手法を用いて，${\displaystyle ad+bc=6}$ を満たすものを見つける．

${\displaystyle \{\begin{array}{c}a=1\\ c=1\end{array}}$ ，${\displaystyle \{\begin{array}{c}b=-8\\ d=9\end{array}}$ のとき

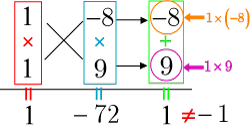
となるので，失敗である．

${\displaystyle \{\begin{array}{c}a=1\\ c=1\end{array}}$ ，${\displaystyle \{\begin{array}{c}b=8\\ d=-9\end{array}}$ のとき

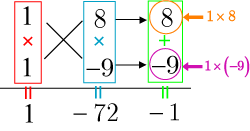
となるので，成功である．

よって，${\displaystyle \{\begin{array}{cc}a=1& b=8\\ c=1& d=-9\end{array}}$ とすればよい．

したがって，${\displaystyle \left(ax+b\right)\left(cx+d\right)}$ に代入すると

${\displaystyle x^2-x-72=\left(x+8\right)\left(x-9\right)}$

ホーム>>カテゴリー分類>>数と式>>問題演習>>因数分解

学生スタッフ作成

最終更新日： 2023年7月20日

[ページトップ]

利用規約

google translate (English version)