|
|||||||||||||
|
|||||||||||||
|
極座標表示におけるラプラシアン (2次元)
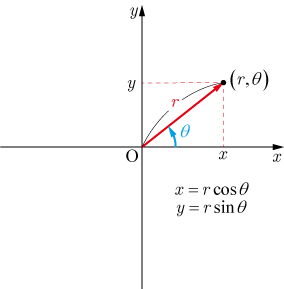
関数ψ=ξ(x,y)ψ=ξ(x,y) において極座標表示x=rcosθx=rcosθ ，y=rsinθy=rsinθ におけるラプラシアンは
Δψ=(∂2∂x2+∂2∂y2)ψΔψ=(∂2∂x2+∂2∂y2)ψ=(∂2∂r2+1r∂∂r+1r2∂2∂θ2)ψ=(∂2∂r2+1r∂∂r+1r2∂2∂θ2)ψ
で与えられる．
■導出手順
与式の左辺の∂2ψ∂x2∂2ψ∂x2
，
∂2ψ∂y2∂2ψ∂y2
を求め，
∂r∂x∂r∂x
，
∂2r∂x2∂2r∂x2
，∂θ∂x∂θ∂x
，∂2θ∂x2∂2θ∂x2
，∂r∂y∂r∂y
，∂2r∂y2∂2r∂y2
，∂θ∂y∂θ∂y
，∂2θ∂y2∂2θ∂y2
を用いて右辺へ式変形する．
■導出
始めに，関数 ψψ をxx で偏微分する．
∂ψ∂x∂ψ∂x =∂ψ∂r∂r∂x+∂ψ∂θ∂θ∂x=∂ψ∂r∂r∂x+∂ψ∂θ∂θ∂x
参考:合成関数の偏導関数
∂2ψ∂x2∂2ψ∂x2 =∂∂x(∂ψ∂x)=∂∂x(∂ψ∂x)
=∂∂x(∂ψ∂r∂r∂x+∂ψ∂θ∂θ∂x)=∂∂x(∂ψ∂r∂r∂x+∂ψ∂θ∂θ∂x)
=∂∂x(∂ψ∂r∂r∂x)+∂∂x(∂ψ∂θ∂θ∂x)=∂∂x(∂ψ∂r∂r∂x)+∂∂x(∂ψ∂θ∂θ∂x)
ここで
より
={∂∂x(∂ψ∂r)}∂r∂x={∂∂x(∂ψ∂r)}∂r∂x+∂ψ∂r{∂∂x(∂r∂x)}+∂ψ∂r{∂∂x(∂r∂x)}+{∂∂x(∂ψ∂θ)}∂θ∂x+{∂∂x(∂ψ∂θ)}∂θ∂x+∂ψ∂θ{∂∂x(∂θ∂x)}+∂ψ∂θ{∂∂x(∂θ∂x)}
さらにここで
∂∂x(∂ψ∂r)∂∂x(∂ψ∂r)={∂∂r∂ψ∂r}∂r∂x+{∂∂θ∂ψ∂r}∂θ∂x={∂∂r∂ψ∂r}∂r∂x+{∂∂θ∂ψ∂r}∂θ∂x=∂2ψ∂r2∂r∂x+∂2ψ∂θ∂r∂θ∂x=∂2ψ∂r2∂r∂x+∂2ψ∂θ∂r∂θ∂x
∂∂x(∂ψ∂θ)∂∂x(∂ψ∂θ)={∂∂r∂ψ∂θ}∂r∂x+{∂∂θ∂ψ∂θ}∂θ∂x={∂∂r∂ψ∂θ}∂r∂x+{∂∂θ∂ψ∂θ}∂θ∂x=∂2ψ∂r∂θ∂r∂x+∂2ψ∂θ2∂θ∂x=∂2ψ∂r∂θ∂r∂x+∂2ψ∂θ2∂θ∂x
より
=(∂2ψ∂r2∂r∂x+∂2ψ∂θ∂r∂θ∂x)∂r∂x=(∂2ψ∂r2∂r∂x+∂2ψ∂θ∂r∂θ∂x)∂r∂x+∂ψ∂r∂2r∂2x+∂ψ∂r∂2r∂2x+(∂2ψ∂r∂θ∂r∂x+∂2ψ∂θ2∂θ∂x)∂θ∂x+(∂2ψ∂r∂θ∂r∂x+∂2ψ∂θ2∂θ∂x)∂θ∂x+∂ψ∂θ∂2θ∂2x+∂ψ∂θ∂2θ∂2x
=∂2ψ∂r2(∂r∂x)2+∂2ψ∂θ∂r∂θ∂x∂r∂x=∂2ψ∂r2(∂r∂x)2+∂2ψ∂θ∂r∂θ∂x∂r∂x+∂ψ∂r∂2r∂x2+∂ψ∂r∂2r∂x2+∂2ψ∂r∂θ∂r∂x∂θ∂x+∂2ψ∂r∂θ∂r∂x∂θ∂x
+∂2ψ∂θ2(∂θ∂x)2+∂2ψ∂θ2(∂θ∂x)2+∂ψ∂θ∂2θ∂x2+∂ψ∂θ∂2θ∂x2
･･････(1)
次に
∂r∂x∂r∂x ， ∂2r∂x2∂2r∂x2 ，∂θ∂x∂θ∂x ，∂2θ∂x2∂2θ∂x2
を用いて(1)を式変形する．
始めに
x=rcosθx=rcosθ ， y=rsinθy=rsinθ
の両辺を2乗して加えると
x2+y2=(rcosθ)2+(rsinθ)2x2+y2=(rcosθ)2+(rsinθ)2
となり，これを整理すると
x2+y2=r2x2+y2=r2 ･･････(2)
また，左辺同士、右辺同士で比をとることにより
yx=rsinθrcosθyx=rsinθrcosθ
となり，これを整理して
tanθ=yxtanθ=yx ･･････(3)
参考：三角関数の相互関係
が得られる．上記の(2)，(3)を用いて
∂r∂x∂r∂x ， ∂2r∂x2∂2r∂x2 ，∂θ∂x∂θ∂x ，∂2θ∂x2∂2θ∂x2
を求める．
(2)の両辺をxx で微分して
2x2x =2r∂r∂x=2r∂r∂x
∂r∂x∂r∂x =xr=xr =rcosθr=rcosθr =cosθ=cosθ ･･････(4)
が得られる． (3)の両辺をxで微分して
1cos2θ∂θ∂x1cos2θ∂θ∂x =y(−1x2)=y(−1x2)
(tan2θ+1)∂θ∂x(tan2θ+1)∂θ∂x =−yx2=−yx2
(y2x2+1)∂θ∂x(y2x2+1)∂θ∂x =−yx2=−yx2
(y2+x2x2)∂θ∂x(y2+x2x2)∂θ∂x =−yx2=−yx2
(r2x2)∂θ∂x(r2x2)∂θ∂x =−yx2=−yx2
∂θ∂x∂θ∂x =−yr2=−yr2 =−rsinθr2=−rsinθr2 =−sinθr=−sinθr ･･････(5)
が得られる．
∂2r∂x2∂2r∂x2=∂∂x(∂r∂x)=∂∂x(∂r∂x)
(4)を代入して
=∂∂xcosθ=∂∂xcosθ =∂∂rcosθ∂r∂x+∂∂θcosθ∂θ∂x=∂∂rcosθ∂r∂x+∂∂θcosθ∂θ∂x =−sinθ∂θ∂x
(5)を代入して
=−sinθ(−sinθr) =sin2θr ･･････(6)
が得られる．
∂2θ∂x2 =∂∂x(∂θ∂x)
(5)を代入して
=∂∂x(−sinθr) =∂∂r(−sinθr)∂r∂x+∂∂θ(−sinθr)∂θ∂x
(4)，(5)より
=sinθcosθr2+cosθsinθr2 =2sinθcosθr2 ･･････(7)
(4)～(7)を用いて(1)を整理すると
∂2ψ∂x2 =∂2ψ∂r2cos2θ+∂2ψ∂θ∂r(−sinθr)cosθ +∂ψ∂rsin2θr+∂2ψ∂r∂θcosθ(−sinθr) +∂2ψ∂r2sin2θr2+∂ψ∂θ2sinθcosθr2 ･･････(8)
次に，関数 ψ をy で偏微分する．
∂ψ∂y =∂ψ∂r∂r∂y+∂ψ∂θ∂θ∂y
参考:合成関数の偏導関数
y に関しても x と同様に計算して
∂2ψ∂y2 =∂2ψ∂r2(∂r∂y)2+∂2ψ∂θ∂r∂θ∂y∂r∂y+∂ψ∂r∂2r∂y2+∂2ψ∂r∂θ∂r∂y∂θ∂y+∂2ψ∂θ2(∂θ∂y)2+∂ψ∂θ∂2θ∂y2 ･･････(9)
また，(2)，(3)を用いて
∂r∂y ， ∂2r∂y2 ， ∂θ∂y ， ∂2θ∂y2
を求める．
∂r∂y は (4) と同様に計算して
∂r∂y =sinθ ･･････(10)
(3)より
tanθ=yx
これを y で微分して
1cos2θ∂θ∂y =1x
(tan2θ+1)∂θ∂y =1x
(y2x2+1)∂θ∂y =1x
(y2+x2x2)∂θ∂y =1x
(r2x2)∂θ∂y =1x
∂θ∂y =xr2 =rcosθr2 =cosθr ･･････(11)
∂2r∂y2=∂∂y(∂r∂y)
(10)を代入して
=∂∂ysinθ =cosθ∂θ∂y
(11)を代入して
=cos2θr ･･････(12)
∂2θ∂y2 は(7)と同様に計算して
∂2θ∂y2 =−2sinθcosθr2 ･･････(13)
(10)～(13)を用いて(9)を整理すると
∂2ψ∂y2=∂2ψ∂r2sin2θ+∂2ψ∂θ∂r(cosθr)sinθ∂2ψ∂y2+∂ψ∂rcos2θr+∂2ψ∂r∂θsinθ(cosθr)
+∂2ψ∂θ2cos2θr2+∂ψ∂θ(−2sinθcosθr2)
･･････(14)
ここで(8)，(14)より，
∂2ψ∂x2+∂2ψ∂y2
=∂2ψ∂r2+1r∂ψ∂r+1r2∂2ψ∂θ2=(∂2∂r2+1r∂∂r+1r2∂2∂θ2)ψ
となる．よって示された．
ホーム>>カテゴリー別分類>>微分>>偏微分>>極座標表示におけるラプラシアン(2次元)
最終更新日：2023年1月17日
