|
|||||||||||||
|
|||||||||||||
|
関連するページを見るにはこの知識グラフを利用してください.
微分形式
 関数
において,変数
の微小の増分
に対して,
を
の微分といい,
で表す.
関数
において,変数
の微小の増分
に対して,
を
の微分といい,
で表す.
・・・・・・(1)
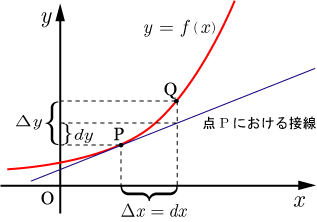
変数 の微小の増分 , 変数 の微小の増分 に対応する の微小の増分 , の微分 , の微分 の関係を右図に示す.
の値が小さくなるにしたがって, の値は1に近づく. すなわち, と が等しくなる.
また,重要な関係式として,
・・・・・・(2)
がある.
■ の微分 について
は独立変数なので をそのまま対応させる関数 とすることにより の微分 について考えてみる.
という関数においては, となるので(1)より,
・・・・・・(3)
となる.さらに より となるので(3)は,
・・・・・・(4)
となる.すなわち,
変数 の微分 は変数 の微小の増分 のことである.
(1),(4)より,
・・・・・・(5)
となる.また, より,
・・・・・・(2)
となる.
また, なので(5)より,
・・・・・・(6)
と表すことができる.
ここで示した,, , , を微分形式という.
最終更新日: 2025年4月25日