グラフの凹凸 (convex upward/downward)

関数 $y = f (x)$ が $x$ のある区間で2次導関数 $f^{″} (x)$ をもつとする．この区間で $f^{″} (x) > 0$ であれば， $x$ の増加に伴い， $f^{'} (x)$ は増加していく，つまり接線の傾きが増加していくので，この区間におけるグラフは下に凸 (convex downward) の形になる．この区間で $f^{″} (x) < 0$ であれば， $x$ の増加に伴い，接線の傾きは減少していくので，この区間におけるグラフは上に凸 (convex upward) の形になる．

$f^{″} (x) > 0$ となる区間において，曲線

$y = f (x)$ は下に凸である．

ii)

$f^{″} (x) < 0$ となる区間において，曲線

$y = f (x)$ は上に凸である．

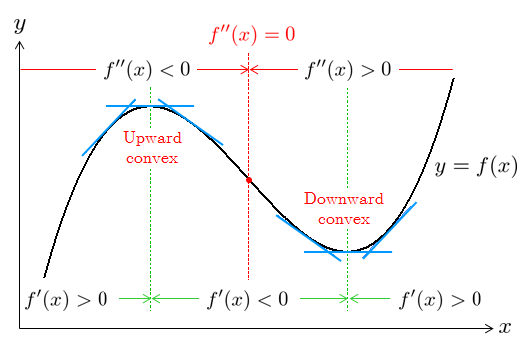
したがって，グラフの凹凸を知るためには， $f^{″} (x)$ の符号を調べればよいということが分かる．また，グラフの凹凸が変わる点では， $f^{″} (x) = 0$ となっている（変曲点）．

下に凸のことを上に凹 (concave upward)，上に凸のことを下に凹 (concave downward)ともいい，一般にある区間で下に凸のグラフとなる関数を凸関数 (convex function)，上に凸（下に凹）のグラフとなる関数を凹関数 (concave function)と呼ぶ．

■第2次導関数まで使った増減表

$x$	$\dots$	$α$	$\dots$	$c$	$\dots$	$β$	$\dots$
$f^{'} (x)$	$+$	$0$	$-$	$-$	$-$	$0$	$+$
$f^{″} (x)$	$-$	$-$	$-$	$0$	$+$	$+$	$+$
$f (x)$		極大値		$f (c)$		極小値

第2次導関数の増減表では，グラフの曲線の曲がり方も含めた矢印，，，を使う．

ホーム>>カテゴリー分類>>微分>>グラフの凹凸

最終更新日：2025年2月21日