合成関数の導関数
, のとき,後の式を前の式に代入すると, となる.これを, ,
の合成関数という.合成関数の導関数は,
あるいは,
(
を代入すると
)
となる.
→合成関数を微分する手順
■導出
合成関数を導関数の定義にしたがって微分する.
ここで, とおくと, となる.よって,
ならば, となる.よって,
導関数を参照
合成関数の導関数を以下のように表す場合もある.
,,
であるので,
となる.
●グラフを用いた合成関数の導関数の説明
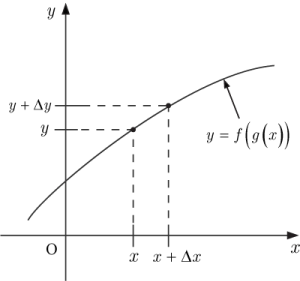
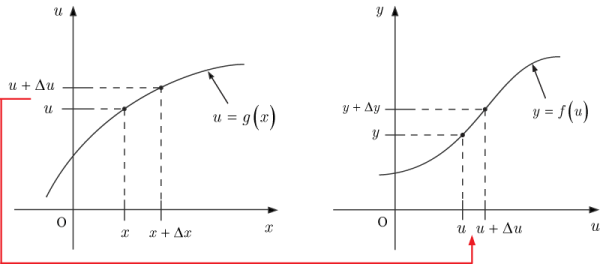
である.
のとき
である.よって
ホーム>>
カテゴリー分類>>
微分>>合成関数の導関数
最終更新日:
2024年5月17日

