平均変化率
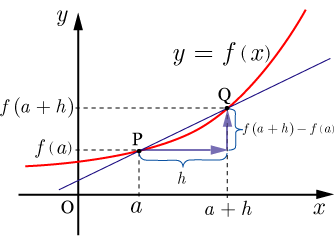 関数 の の値が,から に変化したとき,の変化量を の増加量で割ったものを平均変化率と言う.よって,平均変化率を式で表すと,
関数 の の値が,から に変化したとき,の変化量を の増加量で割ったものを平均変化率と言う.よって,平均変化率を式で表すと,
・・・・・・(1)
となる.図を使って説明すると,平均変化率は直線PQの傾きになる.
関数
の の値が, からに変化したときの平均変化率は,
・・・・・・(2)
となる.((2)は として(1)をかきかえて得られる.)
■具体例
関数
の の値が,2から4に変化したときの平均変化率を求める.
平均変化率の定義式(2)より,
よって,平均変化率は6となる.
ホーム>>カテゴリー分類>>微分>>平均変化率
最終更新日:
2024年5月17日