関連するページを見るにはこのグラフ図を利用してください．

ロピタルの定理

関数${\displaystyle f\left(x\right)}$，${\displaystyle g\left(x\right)}$が下記に示すi，ii，iiiの条件を満たし，${\displaystyle \underset{x\to a}{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\frac{0}{0},\frac{\infty }{\infty }}$の不定形で，${\displaystyle \underset{x\to a}{\lim }\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}}$ が収束，あるいは，${\displaystyle \pm \infty }$ のとき

${\displaystyle \underset{x\to a}{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\underset{x\to a}{\lim }\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}}$

が成り立つ．

1. ${\displaystyle a}$ を含む開区間I( ${\displaystyle a}$ を除くことも可能である)で，関数${\displaystyle f\left(x\right)}$ ，${\displaystyle g\left(x\right)}$ が微分可能で， ${\displaystyle g^{\prime }\left(x\right)\ne 0}$ である．

2. ${\displaystyle \underset{x\to a}{\lim }f\left(x\right)=0}$ ，${\displaystyle \underset{x\to a}{\lim }g\left(x\right)=0}$ ，あるいは，${\displaystyle \underset{x\to a}{\lim }f\left(x\right)=\pm \infty }$ ，${\displaystyle \underset{x\to a}{\lim }f\left(x\right)=\pm \infty }$ である．

3. ${\displaystyle \underset{x\to a}{\lim }\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}}$ が存在(${\displaystyle \pm \infty }$ でもよい)する．

■証明

I．${\displaystyle a}$ を含む開区間Iにおいて，関数${\displaystyle f\left(x\right)}$ ，${\displaystyle g\left(x\right)}$ が微分可能，${\displaystyle g^{\prime }\left(x\right)\ne 0}$ で，${\displaystyle f\left(a\right)=0}$ ，${\displaystyle g\left(a\right)=0}$，かつ，${\displaystyle \underset{x\to a}{\lim }\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}}$ が存在する特殊な場合

${\displaystyle f\left(a\right)=0}$ ，${\displaystyle g\left(a\right)=0}$ より以下のように式を変形することができる．

${\displaystyle \underset{x\to a}{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\underset{x\to a}{\lim }\frac{f\left(x\right)-f\left(a\right)}{g\left(x\right)-g\left(a\right)}}$${\displaystyle =\underset{x\to a}{\lim }\frac{\frac{f\left(x\right)-f\left(a\right)}{x-a}}{\frac{g\left(x\right)-g\left(a\right)}{x-a}}}$

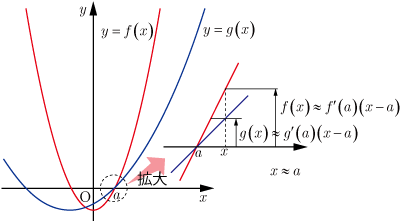微分係数の定義式より

${\displaystyle =\frac{f^{\prime }\left(a\right)}{g^{\prime }\left(a\right)}}$

${\displaystyle a}$ を含む開区間Iにおいて，関数${\displaystyle f\left(x\right)}$ ，${\displaystyle g\left(x\right)}$ が微分可能より${\displaystyle f^{\prime }\left(x\right)}$ ，${\displaystyle g^{\prime }\left(x\right)}$ が連続であることから

${\displaystyle =\frac{\underset{x\to a}{\lim }{f}^{\prime }\left(x\right)}{\underset{x\to a}{\lim }{g}^{\prime }\left(x\right)}}$${\displaystyle =\underset{x\to a}{\lim }\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}}$

となる．

II．${\displaystyle a}$ を含む開区間I(${\displaystyle a}$ を除くことも可能である)において，関数${\displaystyle f\left(x\right)}$ ，${\displaystyle g\left(x\right)}$ が微分可能，${\displaystyle g^{\prime }\left(x\right)\ne 0}$ で，${\displaystyle \underset{x\to a}{\lim }f\left(x\right)=0}$，${\displaystyle \underset{x\to a}{\lim }g\left(x\right)=0}$ではあるが ${\displaystyle f\left(a\right)=0}$ ，${\displaystyle g\left(a\right)=0}$とならず，かつ，${\displaystyle \underset{x\to a}{\lim }\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}}$ が存在する特殊な場合

以下に示す関数を導入する．

${\displaystyle F\left(x\right)=\left\{\begin{array}{ll}f\left(x\right)\hfill & x\ne a\hfill \\ 0\hfill & x=a\hfill \end{array}\right.}$，${\displaystyle G\left(x\right)=\left\{\begin{array}{ll}g\left(x\right)\hfill & x\ne a\hfill \\ 0\hfill & x=a\hfill \end{array}\right.}$　･･････(1)

（${\displaystyle F\left(x\right)}$ ，${\displaystyle G\left(x\right)}$ は${\displaystyle x=a}$ で連続）

証明Iより

${\displaystyle \underset{x\to a}{\lim }\frac{F\left(x\right)}{G\left(x\right)}=\underset{x\to a}{\lim }\frac{F^{\prime }\left(x\right)}{G^{\prime }\left(x\right)}}$　･･････(2)

が成り立つ．

・ ${\displaystyle x>a}$ の場合について

(1)より

${\displaystyle F\left(x\right)=f\left(x\right)}$，${\displaystyle G\left(x\right)=g\left(x\right)}$

となり，(2)を(3)のように書き換えることができる.

${\displaystyle \underset{x\to a+0}{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\underset{x\to a+0}{\lim }\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}}$　･･････(3)

・ ${\displaystyle x<a}$ の場合について

(1)より

${\displaystyle F\left(x\right)=f\left(x\right)}$，${\displaystyle G\left(x\right)=g\left(x\right)}$

となり，(2)を(4)のように書き換えることができる.

${\displaystyle \underset{x\to a-0}{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\underset{x\to a-0}{\lim }\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}}$　･･････(4)

(3)と(4)を合わせると

${\displaystyle \underset{x\to a}{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\underset{x\to a}{\lim }\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}}$

が成り立つ．

III．${\displaystyle a}$ を含む開区間I(${\displaystyle a}$ を除くことも可能である)において，関数${\displaystyle f\left(x\right)}$ ，${\displaystyle g\left(x\right)}$ が微分可能，${\displaystyle g^{\prime }\left(x\right)\ne 0}$ で，${\displaystyle \underset{x\to a}{\lim }f\left(x\right)=\pm \infty }$ ，${\displaystyle \underset{x\to a}{\lim }g\left(x\right)=\pm \infty }$，かつ，${\displaystyle \underset{x\to a}{\lim }\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}}$ が存在する(${\displaystyle \pm \infty }$ でもよい)場合

${\displaystyle \underset{x\to a}{\lim }\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}=\alpha }$　･･････(5)

とおく．(5)をε-δ論法で言い換えると

「${\displaystyle \epsilon >0}$ を任意に1つ選び固定する．この${\displaystyle \epsilon }$ に対して，${\displaystyle 0<\left|x-a\right|<\delta \Rightarrow \left|\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}-\alpha \right|<\epsilon }$ を満たすある正の数${\displaystyle \delta }$ が存在する．」　･･････(6)

となる．

・ ${\displaystyle a<x<b_1}$ の場合

閉区間${\displaystyle \left[x,b_1\right]}$でコーシーの平均値の定理を適用すると

${\displaystyle \frac{f\left(x\right)-f\left(b_1\right)}{g\left(x\right)-g\left(b_1\right)}=\frac{f^{\prime }\left(c_1\right)}{g^{\prime }\left(c_1\right)}}$　･･････(7)

を満たす${\displaystyle c_1\left(x<c_1<b_1\right)}$ が存在する．

${\displaystyle b_1}$ を${\displaystyle a}$ に近づけていくと，${\displaystyle c_1}$ も${\displaystyle a}$ に近づき，${\displaystyle 0<\left|c_1-a\right|<\delta }$ となる．

このとき，(6)より

${\displaystyle \left|\frac{f^{\prime }\left(c_1\right)}{g^{\prime }\left(c_1\right)}-\alpha \right|<\epsilon }$　･･････(8)

が成り立つ．

(7)を以下のように変形する．

${\displaystyle \frac{f\left(x\right)\left\{1-\frac{f\left(b_1\right)}{f\left(x\right)}\right\}}{g\left(x\right)\left\{1-\frac{g\left(b_1\right)}{g\left(x\right)}\right\}}=\frac{f^{\prime }\left(c_1\right)}{g^{\prime }\left(c_1\right)}}$

${\displaystyle \frac{f\left(x\right)}{g\left(x\right)}·\frac{1-\frac{f\left(b_1\right)}{f\left(x\right)}}{1-\frac{g\left(b_1\right)}{g\left(x\right)}}=\frac{f^{\prime }\left(c_1\right)}{g^{\prime }\left(c_1\right)}}$　･･････(9)

(8)に(9)を代入する．

${\displaystyle \left|\frac{f\left(x\right)}{g\left(x\right)}·\frac{1-\frac{f\left(b_1\right)}{f\left(x\right)}}{1-\frac{g\left(b_1\right)}{g\left(x\right)}}-\alpha \right|<\epsilon }$　･･････(10)

${\displaystyle b_1}$ を固定し${\displaystyle x\to a+0}$ の極限をとる．

${\displaystyle x\to a+0}$ のとき，${\displaystyle f\left(x\right)\to \pm \infty }$ ，${\displaystyle g\left(x\right)\to \pm \infty }$ ，${\displaystyle f\left(b_1\right)}$ ，${\displaystyle g\left(b_1\right)}$ は有限の値なので，${\displaystyle \frac{f\left(b_1\right)}{f\left(x\right)}\to 0}$ ，${\displaystyle \frac{g\left(b_1\right)}{g\left(x\right)}\to 0}$ となり，(10)は

${\displaystyle \left|\frac{f\left(x\right)}{g\left(x\right)}-\alpha \right|<\epsilon }$

となる．よって

${\displaystyle x\to a+0}$ のとき，${\displaystyle 0<\left|c_1-a\right|<\delta \Rightarrow \left|\frac{f\left(x\right)}{g\left(x\right)}-\alpha \right|<\epsilon }$ 　･･････(11)

が成り立つ．

${\displaystyle a<x<c_1<b_1}$より

${\displaystyle 0<\left|c_1-a\right|<\delta \Rightarrow 0<\left|x-a\right|<\delta }$

したがって

${\displaystyle x\to a+0}$ のとき，${\displaystyle 0<\left|x-a\right|<\delta \Rightarrow \left|\frac{f\left(x\right)}{g\left(x\right)}-\alpha \right|<\epsilon }$

すなわち

${\displaystyle \underset{x\to a+0}{\lim }\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}=\alpha }$　のとき，${\displaystyle \underset{x\to a+0}{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\alpha }$ 　･･････(12)

成り立つ

・ ${\displaystyle b_2<x<a}$ の場合

閉区間${\displaystyle \left[b_2,x\right]}$ でコーシーの平均値の定理を適用すると

${\displaystyle \frac{f\left(b_2\right)-f\left(x\right)}{g\left(b_2\right)-g\left(x\right)}=\frac{f^{\prime }\left(c_2\right)}{g^{\prime }\left(c_2\right)}}$　･･････(13)

を満たす${\displaystyle c_2\left(x<c_2<b_2\right)}$が存在する．

${\displaystyle b_2}$ を${\displaystyle a}$ に近づけていくと，${\displaystyle c_2}$ も${\displaystyle a}$ に近づき，${\displaystyle 0<\left|c_2-a\right|<\delta }$ となる．

このとき，(6)より

${\displaystyle \left|\frac{f^{\prime }\left(c_2\right)}{g^{\prime }\left(c_2\right)}-\alpha \right|<\epsilon }$　･･････(14)

が成り立つ．

(13)を以下のように変形する．

${\displaystyle \frac{f\left(x\right)\left\{\frac{f\left(b_2\right)}{f\left(x\right)}-1\right\}}{g\left(x\right)\left\{\frac{g\left(b_2\right)}{g\left(x\right)}-1\right\}}=\frac{f^{\prime }\left(c_2\right)}{g^{\prime }\left(c_2\right)}}$

${\displaystyle \frac{f\left(x\right)}{g\left(x\right)}·\frac{\frac{f\left(b_2\right)}{f\left(x\right)}-1}{\frac{g\left(b_2\right)}{g\left(x\right)}-1}=\frac{f^{\prime }\left(c_2\right)}{g^{\prime }\left(c_2\right)}}$　･･････(15)

(14)に(15)を代入する．

${\displaystyle \left|\frac{f\left(x\right)}{g\left(x\right)}·\frac{\frac{f\left(b_2\right)}{f\left(x\right)}-1}{\frac{g\left(b_2\right)}{g\left(x\right)}-1}-\alpha \right|<\epsilon }$　･･････(16)

${\displaystyle b_2}$ を固定し${\displaystyle x\to a-0}$ の極限をとる．

${\displaystyle x\to a-0}$ のとき，${\displaystyle f\left(x\right)\to \pm \infty }$ ，${\displaystyle g\left(x\right)\to \pm \infty }$ ，${\displaystyle f\left(b_2\right)}$ ，${\displaystyle g\left(b_2\right)}$ は有限の値なので，${\displaystyle \frac{f\left(b_2\right)}{f\left(x\right)}\to 0}$ ，${\displaystyle \frac{g\left(b_2\right)}{g\left(x\right)}\to 0}$ となり，(16)は

${\displaystyle \left|\frac{f\left(x\right)}{g\left(x\right)}-\alpha \right|<\epsilon }$

となる．よって

${\displaystyle x\to a-0}$ のとき，${\displaystyle 0<\left|c_2-a\right|<\delta \Rightarrow \left|\frac{f\left(x\right)}{g\left(x\right)}-\alpha \right|<\epsilon }$ 　･･････(17)

が成り立つ．

${\displaystyle b_2<c_2<x<a}$ より

${\displaystyle 0<\left|c_2-a\right|<\delta \Rightarrow 0<\left|x-a\right|<\delta }$

したがって

${\displaystyle x\to a-0}$ のとき，${\displaystyle 0<\left|x-a\right|<\delta \Rightarrow \left|\frac{f\left(x\right)}{g\left(x\right)}-\alpha \right|<\epsilon }$

すなわち

${\displaystyle \underset{x\to a-0}{\lim }\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}=\alpha }$　のとき，${\displaystyle \underset{x\to a-0}{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\alpha }$ 　･･････(18)

成り立つ

(12)と(18)を合わせると

${\displaystyle \underset{x\to a}{\lim }\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}=\alpha }$ のとき，${\displaystyle \underset{x\to a}{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\alpha }$

すなわち

${\displaystyle \underset{x\to a}{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\underset{x\to a}{\lim }\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}}$ 　･･････(19)

が成り立つ．

IY．${\displaystyle a\to \pm \infty }$ の場合

${\displaystyle t=\frac{1}{x}}$ となる変数${\displaystyle t}$ と${\displaystyle f\left(\frac{1}{t}\right)=H\left(t\right)}$，${\displaystyle g\left(\frac{1}{t}\right)=I\left(t\right)}$ となる関数${\displaystyle H\left(t\right)}$ ，${\displaystyle I\left(t\right)}$ を導入する．

${\displaystyle t\ne 0}$ ，${\displaystyle x\to \pm \infty }$ のとき${\displaystyle t\to \pm 0}$ である．

${\displaystyle H^{\prime }\left(t\right)={\left\{f\left(\frac{1}{t}\right)\right\}}^{\prime }}$${\displaystyle =f^{\prime }\left(\frac{1}{t}\right)\times {\left(\frac{1}{t}\right)}^{\prime }}$${\displaystyle =f^{\prime }\left(\frac{1}{t}\right)\times \left(-\frac{1}{t^2}\right)}$

${\displaystyle I^{\prime }\left(t\right)={\left\{g\left(\frac{1}{t}\right)\right\}}^{\prime }}$${\displaystyle =f^{\prime }\left(\frac{1}{t}\right)\times {\left(\frac{1}{t}\right)}^{\prime }}$${\displaystyle =g^{\prime }\left(\frac{1}{t}\right)\times \left(-\frac{1}{t^2}\right)}$

より

関数${\displaystyle H\left(t\right)}$ ，${\displaystyle I\left(t\right)}$ は0を除く0の近傍で微分可能で，${\displaystyle I\left(t\right)\ne 0}$ である．･･････(20)

また

${\displaystyle \underset{t\to \pm 0}{\lim }\frac{H^{\prime }\left(t\right)}{I^{\prime }\left(t\right)}=\underset{t\to \pm 0}{\lim }\frac{f^{\prime }\left(\frac{1}{t}\right)\left(-\frac{1}{t^2}\right)}{g^{\prime }\left(\frac{1}{t}\right)\left(-\frac{1}{t^2}\right)}}$${\displaystyle =\underset{t\to \pm 0}{\lim }\frac{f^{\prime }\left(\frac{1}{t}\right)}{g^{\prime }\left(\frac{1}{t}\right)}\underset{x\to \pm \infty }{=\lim }\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}}$

より

${\displaystyle \underset{x\to \pm \infty }{\lim }\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}}$が存在すると${\displaystyle \underset{t\to \pm 0}{\lim }\frac{H^{\prime }\left(t\right)}{I^{\prime }\left(t\right)}}$ も存在する．･･････(21)

・ ${\displaystyle \underset{x\to \pm \infty }{\lim }f\left(x\right)=0}$ ， $\underset{x\to \pm \infty }{\lim }g\left(x\right)=0$ の時

${\displaystyle x\to \pm \infty }$ のとき， ${\displaystyle t\to \pm 0}$ となることより

${\displaystyle \underset{t\to \pm 0}{\lim }H\left(x\right)=0}$ ，${\displaystyle \underset{t\to \pm 0}{\lim }I\left(x\right)=0}$ 　･･････(22)

となる．(20)，(21)，(22)より(3)および(4)が適用でき

${\displaystyle \underset{t\to +0}{\lim }\frac{H\left(t\right)}{I\left(t\right)}=\underset{t\to +0}{\lim }\frac{H^{\prime }\left(t\right)}{I^{\prime }\left(t\right)}}$

すなわち

${\displaystyle \underset{x\to \pm \infty }{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\underset{x\to \pm \infty }{\lim }\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}}$　･･････(23)

が得られる．

・${\displaystyle \underset{x\to \pm \infty }{\lim }f\left(x\right)=\pm \infty }$ ， ${\displaystyle \underset{x\to \pm \infty }{\lim }g\left(x\right)=\pm \infty }$ の時

${\displaystyle x\to \pm \infty }$ のとき，${\displaystyle t\to \pm 0}$ となることより

${\displaystyle \underset{t\to \pm 0}{\lim }H\left(x\right)=\pm \infty }$ ，${\displaystyle \underset{t\to \pm 0}{\lim }I\left(x\right)=\pm \infty }$ 　･･････(24)

となる．(20)，(21)，(24)より(12)，(18)が適用でき

${\displaystyle \underset{t\to \pm 0}{\lim }\frac{H\left(t\right)}{I\left(t\right)}=\underset{t\to \pm 0}{\lim }\frac{H^{\prime }\left(t\right)}{I^{\prime }\left(t\right)}}$

すなわち

${\displaystyle \underset{x\to \pm \infty }{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\underset{x\pm \to \infty }{\lim }\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}}$ 　･･････(25)

が得られる．

　

【参考図書】
微分積分キャンパスゼミ　著者：高杉豊，馬場敬之　出版社：マセマ出版社
Calculus 7E 著者：James Stewart　出版社：Brooks/Cole Pub Co

ホーム>>カテゴリー分類>>微分>>ロピタルの定理

最終更新日： 2022年6月28日

　　　　

[ページトップ]

利用規約

google translate (English version)