複素数の積分
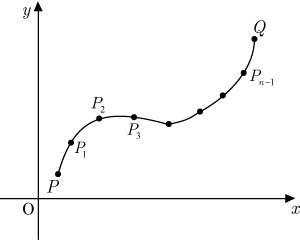
複素平面上の2点
,を結ぶ経路
があり,経路が経路
上の
個の点で
個に分割されているとする.点
側から
個の点を
,
,
,
とし,点
を
,点
を
とも呼ぶことにする.経路
上の一部
と
の間の経路上に点
がある.
点の複素数の値を
,点の複素数の値を
とする.
複素関数
において
(ただし,
)
の値を
と表し,経路
に沿う積分と定義する.
を積分経路という.
曲線
が滑らかな曲線で
と表すことにすると
(ただし
)
となる.
ホーム>>カテゴリー分類>>積分,複素数 >>複素解析>>複素数の積分
最終更新日:
2023年2月28日