|
|||||||||||||
|
|||||||||||||
|
複素数の実数倍
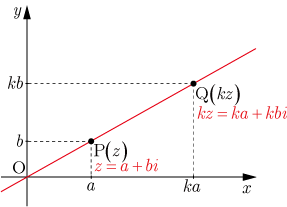
図1
複素数 を 倍( は実数 )した は
となる.複素平面で点 ,点 を表すと図のようになり,原点 ,点 ,点 は,原点 を通る直線上に ある.
となり, の絶対値は の絶対値の 倍になる.言い換えると,線分 の長さは,線分 の長さの 倍である.
■解説
点 から 軸に垂線を下ろし 軸との交点を とし,点 から 軸に垂線を下ろし 軸との交点を とする.図1は の場合,図2は になる.いずれの場合も
となり
∽
である.よって
となり,原点と点 を通る直線の傾きと,原点と点 を通る直線の傾きが等しくなる.じたがって
原点 ,点 ,点 は,原点 を通る直線上に ある.
といえる.
-

図2
-
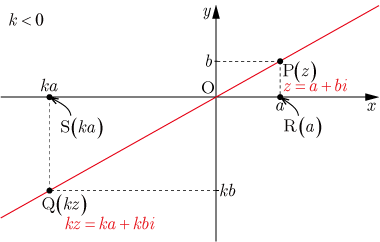
図3
最終更新日: 2025年11月27日