|
|||||||||||||
|
|||||||||||||
|
関連するページを見るにはこのグラフ図を利用してください.
応用分野:
合成関数の2次偏導関数の導出,
合成関数の2次偏導関数の導出,
合成関数の2次偏導関数の導出,
偏微分の基本公式(I)の導出:合成関数,
合成関数を微分する手順,
合成関数の微分のチェーンルール,
対数微分法,
合成関数の導関数,
合成関数の2次偏導関数の導出,
問題リスト←このページに関連している問題です
合成関数
2つの関数
変数
と表される.
今度は,
と表される.
(2)の変数
と表される.すなわち,変数
と表す.
この合成関数の概念を図で表すと下図のようになる.
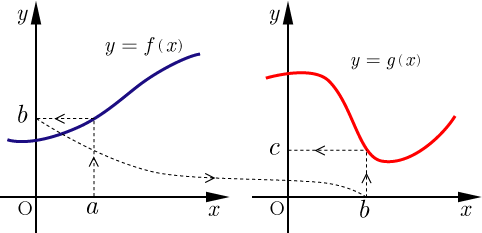
合成写像を参照のこと
最終更新日 2023年4月18日