グラフの拡大→グラフの平行移動した関数

多くの関数のグラフは基本となる関数のグラフを原点を中心として拡大した後，平行移動することによって得られる ．関数 ${\displaystyle y=f\left(x\right)}$ のグラフの原点を中心として $x$ 軸方向に  $c$  倍 ， $y$  軸方向に $d$  倍 した後， $x$ 軸方向に $a$ ， $y$  軸方向に $b$ 平行移動（移動距離は軸の正の方向を正とする）したグラフを表す関数は

${\displaystyle \frac{y-b}{d}=f\left(\frac{x-a}{c}\right)}$ ･･････(1)

となる．

■式の導出

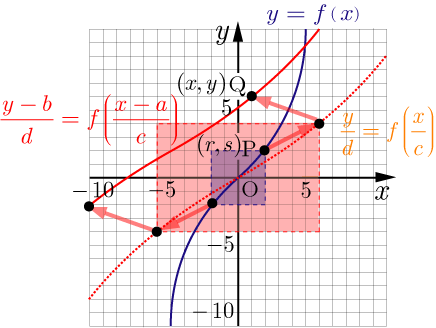${\displaystyle y=f\left(x\right)}$ 上の点 $\text{P}$ がこの変換により移動した先を点 $\text{Q}$ とし，点 $\text{P}$ ， $\text{Q}$ の座標をそれぞれ ${\displaystyle \left(r,s\right)}$ ， $\left(x,y\right)$ とする．点 $\text{Q}$ の $x$ 座標の値は点 $\text{P}$ の $x$ 座標の値 $r$ を $c$ 倍し更に $a$ 加えたものとなり，点 $\text{Q}$ の $y$ 座標の値は点 $\text{P}$ の $y$ 座標の値 $s$ を $d$ 倍し更に $b$ 加えたものである．すなわち

${\displaystyle \{\begin{array}{l}x=cr+a\\ y=ds+b\end{array}}$ ${\displaystyle \to \left(x,y\right)=\left(cr+a,ds+b\right)}$ ･･････(2)

の関係がある．これは点 $\text{Q}$ を点 $\text{P}$ の座標の値を用いて表しているが，逆に点 $\text{P}$ の座標を，点 $\text{Q}$ の座標の値 $x$ ， $y$ を使って表すと

${\displaystyle \{\begin{array}{l}r=\frac{x-a}{c}\\ s=\frac{y-b}{d}\end{array}}$ ${\displaystyle \to \left(x,y\right)=\left(\frac{x-a}{c},\frac{y-b}{d}\right)}$ ･･････(3)

となる．点 $\text{P}$ は ${\displaystyle y=f\left(x\right)}$ 上の点であるので

${\displaystyle s=f\left(r\right)}$ ･･････(4)     

の関係がある．(4)の $r$ ， $s$ に(3)の ${\displaystyle r=\frac{x-a}{c}}$ ， ${\displaystyle s=\frac{y-b}{d}}$ の関係を代入すると

${\displaystyle \frac{y-b}{d}=f\left(\frac{x-a}{c}\right)}$ ･･････(1)  

となる．(1)は $x$ と $y$  の関係を表している．すなわち，この(1)が $y=f\left(x\right)$ のグラフを 拡大後平行移動したグラフを表す関数 である．  

ホーム>>カテゴリー分類>>関数>>グラフの拡大→平行移動した関数

最終更新日： 2025年4月22日

[ページトップ]

利用規約

google translate (English version)