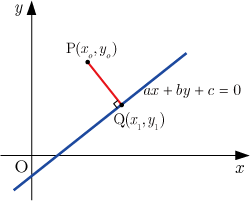
垂線の長さ（点と直線の距離）

点${\displaystyle \left(x_0,y_0\right)}$から直線 ${\displaystyle ax+by+c=0}$への垂線の長さ（言い換えると 点 ${\displaystyle \left(x_0,y_0\right)}$と直線 $ax+by+c=0$との距離）は

${\displaystyle \frac{\left|a{x}_0+b{y}_0+c\right|}{\sqrt{a^2+b^2}}}$

となる．

■導出計算

点${\displaystyle \left(x_0,y_0\right)}$を${\displaystyle \text{P}}$ 点とする．この${\displaystyle \text{P}}$ 点から直線 ${\displaystyle ax+by+c=0}$へ下ろした垂線の足を点${\displaystyle \text{Q}}$ とし，その座標を$\left(x_1,y_1\right)$をとする．垂線の長さ${\displaystyle \text{PQ}}$ は

${\displaystyle \text{PQ}=\left|\stackrel{⟶}{\text{PQ}}\right|=\sqrt{{\left(x_1-x_0\right)}^2+{\left(y_1-y_0\right)}^2}}$    ${\displaystyle \left(\because \stackrel{⟶}{\text{PQ}}=\left(x_1-x_0,y_1-y_0\right)\right)}$ ･･････(1)

次に，直線の方向ベクトル${\displaystyle \overrightarrow{m}}$ を求める．

${\displaystyle y=-\frac{a}{b}x-\frac{c}{b}}$ より
${\displaystyle \overrightarrow{m}=\left(1,-\frac{a}{b}\right)}$

${\displaystyle \overrightarrow{m}}$ と$\stackrel{⟶}{\text{PQ}}$ のなす角は90°より

${\displaystyle \stackrel{⟶}{\text{PQ}}·\overrightarrow{m}}$${\displaystyle =\left(x_1-x_0\right)·1+\left(y_1-y_0\right)·\left(-\frac{a}{b}\right)}$${\displaystyle =0}$

よって，

${\displaystyle x_1-x_0=\left(y_1-y_0\right)·\left(\frac{a}{b}\right)}$   ･･････(2)

(1)に(2)を代入すると

${\displaystyle \text{PQ}}$${\displaystyle =\sqrt{{\left(y_1-y_0\right)}^2\frac{a^2+b^2}{b^2}}}$

${\displaystyle =\sqrt{{\left\{\left(y_1-y_0\right)·\left(\frac{a}{b}\right)\right\}}^2+{\left(y_1-y_0\right)}^2}}$   ･･････(3)

次に，${\displaystyle y_1}$ の消去を図る．点Qが直線上にあることより

${\displaystyle a{x}_1+b{y}_1+c=0}$

よって

${\displaystyle x_1=-\frac{b}{a}{y}_1-\frac{c}{a}}$   ･･････(4)

(4)を(2)に代入すると

${\displaystyle -\frac{b}{a}{y}_1-\frac{c}{a}-x_0=\left(y_1-y_0\right)·\left(\frac{a}{b}\right)}$
${\displaystyle \left(-\frac{b}{a}-\frac{a}{b}\right)y_1=x_0-\frac{a}{b}{y}_0+\frac{c}{a}}$
${\displaystyle -\frac{a^2+b^2}{ab}{y}_1=x_0-\frac{a}{b}{y}_0+\frac{c}{a}}$
${\displaystyle y_1=\frac{-1}{a^2+b^2}\left(ab{x}_0-a^2{y}_0+bc\right)}$

よって

${\displaystyle y_1-y_0}$${\displaystyle =\frac{-1}{a^2+b^2}\left(ab{x}_0-a^2{y}_0+bc\right)-y_0}$

${\displaystyle =\frac{-1}{a^2+b^2}\left(ab{x}_0+b^2{y}_0+bc\right)}$

${\displaystyle =\frac{-b}{a^2+b^2}\left(a{x}_0+b{y}_0+c\right)}$   ･･････（5）

(5)を(3)代入して

${\displaystyle \text{PQ}}$ ${\displaystyle =\sqrt{{\left\{\frac{-b}{a^2+b^2}\left(a{x}_0+b{y}_0+c\right)\right\}}^2\frac{a^2+b^2}{b^2}}}$ ${\displaystyle =\sqrt{\frac{{\left(a{x}_0+b{y}_0+c\right)}^2}{a^2+b^2}}}$ ${\displaystyle =\frac{\left|a{x}_0+b{y}_0+c\right|}{\sqrt{a^2+b^2}}}$

が得られる．

 

●別解

 

ホーム>>カテゴリー別分類>>幾何>>垂線の長さ（点と直線の距離）

最終更新日： 2023年2月22日